C5: Le théorème de la limite central et les méthodes inductives reliées
Section 1. Les hommes sont-ils vraiment plus grands que les femmes?
La réponse est non.
Si, lorsque l’on pose la question « Est-ce que les hommes sont plus grands que les femmes? », on veut en réalité savoir « Est-ce que tous les hommes sont plus grands que toutes les femmes? », on voit bien que la réponse est non car il existe moult femmes bien plus grandes que des hommes. La question pourrait être entendue comme « Est-ce qu’il existe un homme plus grand que toutes les femmes? » ou encore « Est-ce tous les hommes sont plus grands qu’une femme? », auquel cas le livre des records Guinness semble dire oui (le plus grand humain adulte jamais mesuré est un homme alors que le plus petit est une femme).
La difficulté dans la question réside dans le passage du particulier à l’universel. La population testée contient un grand nombre d’individu et il faut spécifier comment ces individualités sont insérées dans la question.
Souvent, nos questions portent sur l’individu moyen. Notre question ci-haut devient « Est-ce que la taille moyenne des hommes est supérieure à la taille moyenne des femmes? » (auquel cas la réponse est oui). Bien que l’on n’y pense plus, ce glissement vers « l’individu moyen » ne va pas de soi. Comme on l’a vu plus haut, on peut aussi s’intéresser à l’individu extrême. De plus, il semble que les enfants et les sociétés tribales ne vont réfléchir à la question qu’en terme d’exemples et de contre-exemples. Finalement, l’individu moyen n’existe peut-être pas. Pour ces raisons, il est important dans l’énoncé d’une hypothèse de recherche de bien préciser que l’on fait référence à la moyenne. Cette section décrit plusieurs tests portant sur une ou deux moyennes.
Section 2. Test paramétrique sur la moyenne (σ connu)
Au cours précédent, nous avons vu un test sur une tendance centrale: le test de la médiane. Or, la médiane n’est pas très souvent utilisée en statistique: (1) C’est une mesure moins intuitive que la moyenne. (2) Les tests de la médiane ne sont pas très puissants (i.e. ils ne discriminent pas beaucoup). Pour cette raison, beaucoup de chercheurs vont plutôt utiliser des tests des moyennes. Pour qu’un test de la moyenne soit possible, il faut qu’il n’y ait pas trop de données extrêmes, ce qui n’était pas le cas avec l’exemple des revenus du cours précédent.
2.1. Idée du test
Le test que nous présentons ici n’est presque jamais utilisé parce qu’il est basé sur un postulat beaucoup trop restrictif. Étant donné qu’il utilise la normalisation (transformation en cote z), on l’appelle parfois un test z. Nous le décrivons ici car une technique presque identique est à la base du test t, un test de la moyenne très populaire. De plus, il permet d’introduire la notion d’erreur type.
Imaginons une situation où nous avons mesuré la taille de 250 personnes. Supposons de plus que la distribution des tailles dans la population soit normale et que l’écart type soit de 15 cm. Dans ce cas, si notre hypothèse est que la taille moyenne de la population est de 1.65, nous devrions obtenir de notre échantillon une valeur proche. Si nous transformons ![]() en score z, le résultat obtenu ne devrait pas dévier significativement de zéro. L’importance de cette déviation (son improbabilité) se mesure facilement puisque le score z suit parfaitement une loi normale N(0, 1) (comme nous l’avons vu au cours 3). Si la déviation est improbablement grande ou petite, notre hypothèse doit être incorrecte.
en score z, le résultat obtenu ne devrait pas dévier significativement de zéro. L’importance de cette déviation (son improbabilité) se mesure facilement puisque le score z suit parfaitement une loi normale N(0, 1) (comme nous l’avons vu au cours 3). Si la déviation est improbablement grande ou petite, notre hypothèse doit être incorrecte.
Une dernière subtilité doit nous retenir, qui est suffisamment importante pour en faire un point en soi. Elle concerne l’écart type à utiliser quand nous allons normaliser.
2.2. Écart type et erreur type
En fait, ce que nous voulons normaliser dans ce test, ce n’est pas chaque donnée brute Xi mais uniquement la moyenne ![]() . Donc, pour bien faire les choses, il faudrait diviser la différence
. Donc, pour bien faire les choses, il faudrait diviser la différence ![]() – μ par l’écart type de
– μ par l’écart type de ![]() . La seule façon que nous avons de calculer Var(
. La seule façon que nous avons de calculer Var( ![]() ) serait de prendre plusieurs échantillons puis de calculer la variance entre les différentes moyennes. En fait, c’est comme si l’on bâtissait un échantillon
) serait de prendre plusieurs échantillons puis de calculer la variance entre les différentes moyennes. En fait, c’est comme si l’on bâtissait un échantillon ![]() contenant {
contenant { ![]() 1,
1, ![]() 2,
2, ![]() 3, …,
3, …, ![]() n}. Évidement, dans la pratique, nous n’avons pas le loisir de constituer plusieurs échantillons uniquement pour connaître le dénominateur dans la procédure de normalisation. Heureusement, la statistique peut résoudre ce problème. Rappelez-vous la formule théorique sur la variance que nous avons vue au cours 2 : Var(X) = E(X2) – E2(X). Cette formule s’applique aussi pour
n}. Évidement, dans la pratique, nous n’avons pas le loisir de constituer plusieurs échantillons uniquement pour connaître le dénominateur dans la procédure de normalisation. Heureusement, la statistique peut résoudre ce problème. Rappelez-vous la formule théorique sur la variance que nous avons vue au cours 2 : Var(X) = E(X2) – E2(X). Cette formule s’applique aussi pour ![]() :
:
![]()
Si on détaille le premier terme de la soustraction, on obtient :

On a vu au cours 2 que σ2 =E(X2)−E2(X)=E(X2)−μ2, ce qui implique par simple réarrangement que E(X2 ) = σ 2 + μ 2 . De plus, E(XX) = E(X)E(X) = μ 2 . Finalement, si une variable i peut prendre toutes les valeurs de 1 à n, et que pour un i donné, la variable j peut prendre toutes les valeurs de 1 à i exclusivement, nous nous retrouvons avec n(n-1) / 2 combinaisons de i et de j. Si on intègre tous ces éléments, nous pouvons noter que :
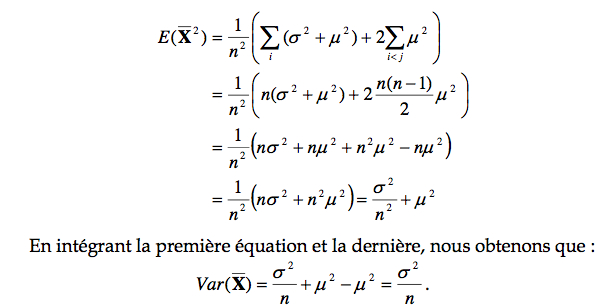
Tout comme pour l’écart type lors du calcul d’une proportion (voir cours 4), l’écart type lors du calcul d’une moyenne est donné par la variance divisée par le nombre d’observations entrant dans le calcul de la variance. On voit ici la consistance des statistiques. Ce résultat est très important puisqu’il montre que plus nous avons d’observations dans notre échantillon, plus la variabilité de la moyenne observée est petite. Autrement dit, plus nous avons d’observations, moins nous risquons de nous tromper sur l’estimation que nous nous faisons de la moyenne de cette population. Ce résultat, omniprésent en statistique, affirme que plus notre échantillon sera grand (ultimement la population entière) plus notre estimation de la moyenne de la population sera certaine. Ce résultat est souvent connu comme la loi des grands nombres.
Cette mesure est un peu une marge d’erreur. En effet, l’écart type signifie (cours 2) que n’importe quelle observation prise au hasard a toute les chances de se trouver à ± un écart type. Similairement, ce résultat-ci indique que pour n’importe quel échantillon pris au hasard, sa moyenne a toute les chances de se retrouver à ± une erreur type de la vraie moyenne de la population. Pour ceux qui ont l’œil, vous reconnaîtrez sans doute l’erreur type introduite à l’encadré .
2.3. Structure du test
a.1. Postulats
Le test est basé sur les postulats que la population est normalement distribuée N( μ, σ ) et que la variance de la population σ2 est connue. Ce dernier point est non plausible.
a.2. Hypothèses et seuil
On veut vérifier si la moyenne de la population μ est bel et bien de μ0, une valeur décidée a priori par le chercheur. L’hypothèse nulle est donc H0 : μ = μ0 . L’hypothèse alternative peut être unicaudale :a)H1:μ>μ0 b)H1:μ<μ0 oubicaudalec)H1:μ≠μ0. Dans l’exemple ci-haut, on opte pour un test bicaudal. Le seuil α est placé à 0.05, parce qu’il n’y a pas de raison de choisir un seuil plus ou moins strict.
a.3. Chercher le test
Le test est de la forme :

Pour laquelle  ~ N(0, 1). Après un examen dans une table N(0,1), on trouve encore la valeur s(α / 2) = 1.96 (une valeur à retenir puisqu’elle va revenir très souvent) pour laquelle 2.5% de la distribution est située en bas de – 1.96 et 2.5% en haut de + 1.96.
~ N(0, 1). Après un examen dans une table N(0,1), on trouve encore la valeur s(α / 2) = 1.96 (une valeur à retenir puisqu’elle va revenir très souvent) pour laquelle 2.5% de la distribution est située en bas de – 1.96 et 2.5% en haut de + 1.96.
a.4. Appliquer le test et conclure
La moyenne empirique obtenue par le chercheur étant de 1.49 m, nous calculons :

qui est considérablement plus grand que notre valeur critique, 1.96. Nous rejetons donc l’hypothèse nulle et concluons qu’il est peu probable que la taille moyenne des individus de notre population soit de 1.65 m.
Dernière chose. Comme vous le voyez, pour un test z (et il en ira de même pour les tests t introduit à la section suivante), le nombre 1.96 est un nombre magique. Introduisons une autre propriété utile de ce nombre : il est presque égal à 2. Cela peut sembler trivial, mais pensons-y une seconde. Supposons que nous avons un graphe illustrant deux moyennes, chacune avec une barre d’erreur de chaque côté, comme dans l’exemple de la Figure 1. L’erreur type au-dessus de blanc monte jusqu’à 17 et l’erreur type sous bleu va jusqu’à 16.

C’est à dire que les barres d’erreurs se chevauchent. Autrement dit, il y a moins de deux erreurs types entre la moyenne des blancs et la moyenne des bleus. Cependant, on a vu que dans un test z (et beaucoup de test t), il faut un écart de presque deux erreurs type pour que la différence soit significative. Ce qui veut dire que si les barres d’erreur se touchent, il y a de très grandes chances que la différence ne soit pas significative. Voilà pourquoi il est important à mon avis de mettre les barres d’erreur type sur les graphes. Évidemment, si le test adéquat n’est pas un test z, il se peut que la différence soit significative même si les barres d’erreur se touchent légèrement (nous en verrons des exemples avec le test t où le nombre d’observations est faible). Cependant, il s’agit dans tous les cas d’une bonne indication pour évaluer l’importance de la différence entre deux histogrammes.
Section 3.Définition du théorème central limite
À la section précédente, nous avons vu le test z qui nécessite des postulats très précis (une population qui soit normale). Cependant, le postulat de normalité est un postulat très fort qui, pour être vérifié, demanderait que l’on mesure la population entière. C’est le genre de chose que l’on veut éviter de faire (sinon, inutile de faire des statistiques!). On aimerait donc que la base sous-jacente à notre test statistique soit un postulat moins fort. Tel est le théorème central limite (ou encore le théorème de la limite centrale).
Ce théorème a été envisagé par Gauss lui-même, le créateur de la distribution normale, aux environs de 1800 dans le cadre de sa théorie des erreurs. Cependant, la preuve complète n’a été obtenue qu’au début de ce siècle, indépendamment par deux mathématiciens, dont Alan Turing, l’inventeur des ordinateurs modernes. Une façon plus claire, et moins mystérieuse de nommer ce théorème serait de l’appeler le théorème de la distribution asymptotique de l’estimateur de la tendance centrale. Par limite, on entend l’hypothèse où le nombre d’éléments serait très grand, qu’on appelle maintenant une hypothèse asymptotique (n >> , soit dans ce contexte, n > 30); par central, on entend l’estimateur de la tendance centrale le plus usuel, la moyenne.
Le nœud de ce théorème est de supposer que l’on ignore la distribution de la population entière. Par contre, le théorème postule que la population a bien une valeur moyenne (inconnue, mais appelons-la μ ) et une variance (inconnue aussi, et notée σ 2 ). Ces postulats sont très naturels et très généraux; on peut s’attendre à ce qu’ils soient vrais de notre population mystère. Par la suite, prenons un échantillon X1 contenant n données brutes, et calculons la moyenne de l’échantillon ![]() 1, puis un second échantillon avec une moyenne
1, puis un second échantillon avec une moyenne ![]() 2, puis un troisième, etc. Maintenant, oublions les données brutes, et considérons que nous avons un échantillon Y ne contenant que des moyennes d’échantillons {
2, puis un troisième, etc. Maintenant, oublions les données brutes, et considérons que nous avons un échantillon Y ne contenant que des moyennes d’échantillons { ![]() 1,
1, ![]() 2,
2, ![]() 3, …,
3, …, ![]() M}. Autrement dit, nous faisons maintenant des statistiques inductives sur des statistiques descriptives plutôt que sur des données brutes. La question est : peut-on savoir comment se distribue Y? La réponse est oui!
M}. Autrement dit, nous faisons maintenant des statistiques inductives sur des statistiques descriptives plutôt que sur des données brutes. La question est : peut-on savoir comment se distribue Y? La réponse est oui!
Ce théorème démontre que Y ~ N(μ, σ / √n), c’est à dire que ![]() la moyenne de Y (la moyenne des moyennes) devrait être de μ, la moyenne réelle de la population, et que l’écart type de Y,
la moyenne de Y (la moyenne des moyennes) devrait être de μ, la moyenne réelle de la population, et que l’écart type de Y, ![]() devrait s’amenuiser lorsque la taille des échantillons individuels est grande.
devrait s’amenuiser lorsque la taille des échantillons individuels est grande.
Il faut bien comprendre la puissance de ce théorème, puissance qui provient du fait que ses postulats de bases sont très peu contraignants : peu importe le type de population et la façon dont se répartissent ses scores, la moyenne obtenue d’un échantillon sera normalement distribuée. Ceci signifie que si l’on extrayait un très grand nombre de moyennes, 95% d’entre elles se trouveront à ± 1.96 écart types. Ceci signifie que l’on peut faire des tests statistiques sur des moyennes, et que le test à utiliser est un test basé sur la normale (un test z).
Un autre résultat important de ce théorème concerne l’erreur type. Nous avons vu que pour la binomiale et pour la distribution normale, l’erreur type (soit l’écart type d’une moyenne) est toujours divisée par √n. Le théorème central limite prouve que c’est aussi le cas pour toutes les autres distributions (peu importe laquelle). Ainsi, peu importe votre population, il est toujours correct de tracer une barre d’erreur autour d’une moyenne sur vos graphes (d’où ma recommandation de toujours le faire).
[Précisons qu’il existe des populations où le théorème central limite ne s’applique pas. Par exemple, il est possible d’imaginer une population où la moyenne serait de 30 quand il y a un nombre pair d’observation, et 40 quand il y a un nombre impair. Dans ce cas, il n’existe pas de moyenne définie pour cette population, et on ne peut donc pas appliquer le théorème. Notons que ce genre de population existe sur papier, mais qu’elles sont rarement présentes dans la nature…]
Le théorème central limite est central en statistiques inductives puisqu’il nous permet de nous débarrasser d’un postulat fort (ou encore d’un postulat restrictif) par un postulat faible. En effet, à la section 5.1, nous avons postulé que la population était belle et bien normalement distribuée. Il s’agit d’un postulat très fort, qui, pour être démontré, exigerait beaucoup de travail. Avec le théorème central limite, le seul postulat dont nous avons besoin est que la population ait une moyenne et une variance. Très peu de chercheurs vont vous disputer ce point. En règle générale, ce postulat est tellement accepté qu’il n’est jamais indiqué explicitement. Étonnement, peu de livres de statistiques vont prendre le temps de décrire ce théorème qui est pourtant une des pierres angulaires des tests sur les moyennes.
Nous ne donnons pas la preuve complète de ce théorème, qui est très complexe.
Section 4.La distribution t
Grâce au théorème central limite, nous sommes en mesure de faire un test sans utiliser le postulat que la population est normalement distribuée (comme ce fut le cas à la section 5.1). Bien que les choses s’améliorent, il reste encore un postulat fait dans la section 5.1 qui est gênant, celui qui dit que la variance de la population d’où est extraite l’échantillon est connu. Bien entendu, si la variance est réellement connue, ceci signifie que la moyenne réelle de la population est aussi connue… Dans les faits, nous sommes contraints d’utiliser la variance non biaisée de l’échantillon.
Dans la section précédente, pour normaliser, nous avons utilisé la formule :

Or, puisque le paramètre σ de la population est inconnu, on divise en fait par une variable aléatoire, une statistique observée dans notre échantillon, l’écart type de l’échantillon. L’équation devient donc :

Alors qu’additionner et soustraire des valeurs ne change pas le fait que ![]() est normalement distribué, diviser une variable aléatoire par une autre peut résulter en une distribution de forme très différente:
est normalement distribué, diviser une variable aléatoire par une autre peut résulter en une distribution de forme très différente:
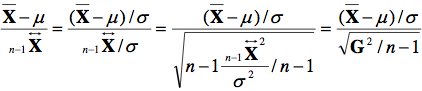
où le numérateur suit une N(0, 1) et le dénominateur est la racine carrée d’une variable χ2 divisée par n – 1 (comme on le verra en 6.3). Dans ce cas-ci, Gosset a démontré aux environs de 1920 quelle est la distribution résultante d’une division d’une moyenne par une variance échantillonale. Il s’agit d’une distribution qu’il a appelé la distribution t, encore connue comme la distribution de Student.
Cette distribution ressemble beaucoup à la distribution normale excepté qu’elle est plus étalée (leptocurtique). Quand le nombre de données brutes dans l’échantillon excède 100, l’incertitude sur la variabilité de la population (estimée par n−1 ![]() ) est tellement réduite que c’est tout comme si nous divisions par σ et le résultat est identique à la distribution normale. Cependant, pour n <<, la kurtose est importante, et il est dangereux d’approximer la distribution par la distribution normale.
) est tellement réduite que c’est tout comme si nous divisions par σ et le résultat est identique à la distribution normale. Cependant, pour n <<, la kurtose est importante, et il est dangereux d’approximer la distribution par la distribution normale.
Comme la forme de la distribution t change avec le nombre de données brutes dans l’échantillon, il est important de faire le test relatif à ce qu’on appelle le nombre de degrés de liberté, une indication du nombre de données brutes dont on dispose. La figure suivante illustre la distribution de t avec 1, 3, et 30 degrés de liberté. Avec un degré de liberté, la distribution est très leptocurtique (kurtose > 3, courbe inférieure).

Section 5. Parallèle entre la section 4 et la section 5
Certains objectifs des tests des sections 4 et 5 sont identiques. Pouvez-vous identifier les postulats qui les distinguent?

Section 6.Test paramétrique sur la moyenne
Le professeur Lear, de la société Asnem défend depuis de nombreuses années l’argument que la valeur obtenue au test de Q. I. est fortement influencée par les expériences vécues par les individus. Dernièrement, il a développé une séquence d’entraînement durant une semaine, et qui, selon ses dires, augmente le Q. I. à 120 points. Il décide donc de lancer un grand programme de recherche pour appuyer sa méthode.
Dans une expérience 1, il applique sa méthode à 40 sujets choisis au hasard dans la population, puis administre un test de Q. I. à la fin de la période. Il obtient les résultats suivant pour son échantillon X = {91, 98, 111, 61, 102, 93, 126, 82, 104, 93, 106, 77, 139, 144, 63, 75, 159, 140, 133, 70, 92, 120, 128, 90, 109, 106, 118, 140, 104, 132, 135, 88, 98, 83, 111, 157, 163, 129, 113, 138}. Considérant le grand nombre de scores qui sont sous 100 (le Q. I. moyen dans la population), peut-on dire que sa méthode est un succès?
6.1. Idée du test
Le test utilisé est basé sur l’idée que la moyenne de notre échantillon est normalement distribuée. En effet, ce résultat est garanti par le théorème central limite puisqu’il ne fait pas de doute que la population entière des Q. I. doit posséder une moyenne et une variance définies. Cependant, comme on ne connaît pas la variance de la population entière des personnes pouvant suivre la séquence d’entraînement, il devient nécessaire d’utiliser la variance de l’échantillon, et donc, le test t devient le test adéquat.
6.2. Structure du test
a.1. Postulats
Théorème central limite et variance inconnue sont les seuls postulats à la base du test, et ils sont très certainement satisfaits dans l’expérience 1.
a.2. Hypothèses et seuil
L’hypothèse nulle précise que le Q. I. n’est pas affecté par la séquence d’entraînement (absence d’effet). Dans ce cas, l’échantillon ayant suivi le traitement devrait toujours avoir un Q. I. de 100. Dans l’expérience 1, on recherche un accroissement du Q. I., et donc un test unicaudal est utilisé. Le chercheur opte pour un seuil standard de 5%. Les hypothèses formelles sont :
H0: ![]() =100
=100
H1 : ![]() > 100
> 100
a.3. Chercher le test
Le test est de la forme :

pour lequel la valeur 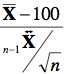 ~ t ( n – 1 ). Dans ce test, il faut, pour obtenir le degré de liberté permettant de savoir quelle forme la distribution de t utiliser, il faut soustraire 1 au nombre d’observations n (40 dans l’expérience 1). Après un regard dans la Table 5, on trouve une valeur critique s(α) égale à 1.686 (puisque le degré de liberté 39 n’est pas tabulé, utilisez le degré de liberté moins strict le plus proche, soit 38 ici).
~ t ( n – 1 ). Dans ce test, il faut, pour obtenir le degré de liberté permettant de savoir quelle forme la distribution de t utiliser, il faut soustraire 1 au nombre d’observations n (40 dans l’expérience 1). Après un regard dans la Table 5, on trouve une valeur critique s(α) égale à 1.686 (puisque le degré de liberté 39 n’est pas tabulé, utilisez le degré de liberté moins strict le plus proche, soit 38 ici).
a.4. Appliquer le test et conclure
Nous calculons la moyenne ![]() = 110.5, et l’écart type non biaisé n−1
= 110.5, et l’écart type non biaisé n−1 ![]() = 26.5. Le dénominateur est comme toujours une erreur type dont la valeur est
= 26.5. Le dénominateur est comme toujours une erreur type dont la valeur est ![]() = 4.19. Le résultat total est donc 2.51. Ce résultat étant nettement supérieur à la valeur critique, on conclue que la séquence d’entraînement résulte dans un quotient intellectuel significativement supérieur à 100. On peut noter au passage que la moyenne du groupe obtenue est aussi significativement inférieure à 120 (faites le test), ce qui semble indiquer que la séquence d’entraînement n’est pas aussi efficace que le proclame le Pr Lear.
= 4.19. Le résultat total est donc 2.51. Ce résultat étant nettement supérieur à la valeur critique, on conclue que la séquence d’entraînement résulte dans un quotient intellectuel significativement supérieur à 100. On peut noter au passage que la moyenne du groupe obtenue est aussi significativement inférieure à 120 (faites le test), ce qui semble indiquer que la séquence d’entraînement n’est pas aussi efficace que le proclame le Pr Lear.
Intervalles de confiance
La relation entre test statistique et intervalle de confiance est toute simple. L’idée d’un test statistique (bicaudal ici) est d’arriver à une relation du genre :
Dans cet exemple, nous utilisons la moyenne, mais bien entendu, le test peut porter sur une autre statistique que la moyenne. L’erreur type (ici noté
) peut parfois être complexe à calculer, mais dans tous les cas est une mesure de la dispersion attendue de la statistique testée. Si le résultat de la formule n’est pas plus grand que s (α), la statistique est considérée comme acceptable (ne conduisant pas à un rejet de H0).
Procédons à une légère modification de la formule ci-haut :
Autrement dit :
Ceci signifie que la vraie valeur de μ doit se trouver incluse entre deux bornes données par la moyenne observée plus ou moins votre seuil de confiance pondéré par l’erreur type. Si votre seuil de rejet est de 5%, l’intervalle de non rejet est de 95%, et la valeur s (α) vous donne un intervalle dans lequel vous êtes à 95% confiant que la vraie valeur μ se trouve incluse. On parle alors d’un intervalle de confiance à 95%.
Quand vous rapportez une moyenne avec la notation
telle que nous l’avons suggéré au cours 2, il ne s’agit pas d’un intervalle de confiance puisque la valeur s (α) n’est pas utilisée. Cependant, pour beaucoup de tests, la valeur s (α) pour un seuil de 95% sera inférieure à deux, ce qui fait qu’à l’œil, on estime rapidement qu’il y a 95% de chance que
soit à ± 2
. Il s’agit d’une indication évidemment, et non pas d’un test formel.
Section 7.Test paramétrique sur deux moyennes
7.1. Test sur groupes indépendants
Une critique qui peut être faite à l’expérience 1 et que le Pr Lear avait prévue est la suivante : Comme on le sait tous, un test de Q. I. est calibré pour donner une moyenne de 100. Cependant, ce calibrage est mené pour une population très restreinte, et pour une époque très précise. Peut être que le test utilisé par le Pr Lear était déjà obsolète, ce qui expliquerait qu’il donne une valeur si élevée. Dans ce cas, la séquence d’entraînement n’a peut être rien à voir avec les résultats obtenus à l’expérience 1. Pour palier à cette critique, le Pr Lear a conduit une expérience 2 dans laquelle il mesure deux groupes de sujets indépendants. Pour le premier groupe, les sujets suivent la séquence d’entraînement prescrite dans la méthode du Pr Lear; le second groupe s’adonne à une activité placebo (mots croisés) pour un même nombre d’heures. Il prédit que le premier groupe aura un score moyen, lorsque mesuré avec un test de Q. I., qui sera significativement supérieur au second groupe.
Les scores obtenus sont : premier groupe, X = {144, 119, 77, 126, 94, 161, 177, 77, 104, 151, 119, 76, 112, 134, 115, 126, 143, 132, 117, 77, 90, 92, 102, 110, 148, 129, 96, 118, 137, 131, 170, 71, 3, 159, 142, 64, 162, 104, 98, 142} et pour le second groupe, Y = {76, 127, 67, 86, 117, 71, 151, 157, 160, 73, 63, 100, 127, 47, 74, 135, 76, 61, 72, 102, 110, 140, 108, 88, 72, 134, 133, 124, 78, 91, 105, 109, 130, 87, 105, 121, 101, 133, 65, 124}.
a.1. Postulats
Une première chose à savoir est que si X est normalement distribué et que Y est aussi normalement distribué, alors une combinaison des deux (tel X + Y) l’est aussi. (Dans le cas de l’addition, en utilisant les relations du cours 2, on voit que la moyenne des scores X + Y est de ![]() +
+ ![]() alors que la variance est de n−1
alors que la variance est de n−1 ![]() + n−1
+ n−1![]() ). Dès lors, puisque selon le théorème central limite, chaque moyenne est normalement distribuée, ce doit être vrai aussi de la différence entre deux moyennes
). Dès lors, puisque selon le théorème central limite, chaque moyenne est normalement distribuée, ce doit être vrai aussi de la différence entre deux moyennes ![]() –
– ![]() .
.
Pour estimer la variance présente dans nos échantillons, nous allons utiliser la passe de mammouth no 1 et combiner les variances pour avoir un estimé unique pour la variance dans
l’échantillon X et dans l’échantillon Y. Posons n−1 ![]() 2 l’estimé de la variance présent dans les deux échantillons, calculé comme une somme pondérée par les degrés de liberté :
2 l’estimé de la variance présent dans les deux échantillons, calculé comme une somme pondérée par les degrés de liberté :

Il ne nous reste plus qu’à combiner les carrés des erreurs type, car une erreur type au carré est additive, tout comme les variances :
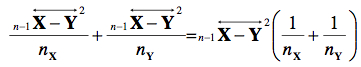
a.2. Hypothèses et seuil
L’hypothèse est que les deux scores ne diffèrent pas alors que l’hypothèse alternative est que le premier groupe est significativement supérieur au second :
H0 : ![]() =
= ![]()
H1 : ![]() >
> ![]()
Une fois encore, un seuil de 5% est utilisé.
a.3. Chercher le test
Le test est de la forme :

pour lequel, en vertu du théorème central limite, la valeur  ~ t ( nX + nY –2). Dans ce cas-ci, nX + nY –2 indique le nombre de degrés de liberté pour le test t à deux groupes indépendants. Dans notre exemple, nX + nY –2 = 78. Après un regard dans la table, on trouve s (α) = 1.665.
~ t ( nX + nY –2). Dans ce cas-ci, nX + nY –2 indique le nombre de degrés de liberté pour le test t à deux groupes indépendants. Dans notre exemple, nX + nY –2 = 78. Après un regard dans la table, on trouve s (α) = 1.665.
a.4. Appliquer le test et conclure
Puisque ![]() = 118.23 et que
= 118.23 et que ![]() = 102.5 et que l’écart type non biaisé est de n−1
= 102.5 et que l’écart type non biaisé est de n−1 ![]() = 29.60 et n−1
= 29.60 et n−1![]() = 29.51, nous calculons le dénominateur avec
= 29.51, nous calculons le dénominateur avec
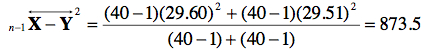
Au total, la formule devient :

7.2. Test sur mesures répétées
Une autre critique qui peut être adressée au Pr Lear concerne son objectivité dans le choix des participants. En principe, les participants doivent être assignés au hasard dans l’une ou l’autre des conditions de l’expérience 2. Cependant, il est possible que des facteurs inconscients ait incité le Pr Lear à assigner les sujets qui semblaient plus intelligents à la condition 1. Bien que le Pr Lear soit certain de ne pas avoir été la victime de ce biais, il a néanmoins procédé à une expérience 3 pour répondre à de possibles critiques.
Dans cette expérience, il a opté pour une expérience du type test-retest, dans laquelle chaque sujet est mesuré après un entraînement sur une tâche placebo et après la séquence d’entraînement, est remesuré. Le sujet ignore lequel des entraînements est le plus efficace.
L’approche test-retest est une approche plus puissante car elle permet d’éliminer une certaine variance. Dans l’expérience 2, une part importante de la variance provient du fait que ce sont des individus différents qui forment les deux groupes. Certains peuvent avoir un Q. I. élevé, d’autres un faible Q. I. et la répartition des Q. I. peut être inégale simplement par pur hasard (erreur d’échantillonnage). Dans cette expérience-ci, le même individu prend place dans les deux groupes. S’il a un Q. I. élevé, son score sera élevé dans les deux tests, peu importe l’efficacité du traitement. Ceci signifie qu’une part de la variabilité est éliminée si on considère un score individuel avant et après.
Les résultats obtenus sont les suivants. Avant la séquence : X = {150, 73, 101, 159, 120, 110, 85, 48, 79, 95, 75, 140, 61, 93, 137, 81, 143, 85, 99, 130, 149, 49, 82, 76, 145, 129, 159, 95, 126, 140, 87, 109, 106, 79, 103, 115, 104, 154, 87, 62}; après la séquence : Y = {152, 67, 103, 193, 141, 53, 84, 14, 84, 92, 123, 177, 50, 84, 171, 78, 171, 105, 53, 137, 223, 52, 109, 61, 147, 137, 161, 141, 129, 187, 146, 117, 118, 107, 154, 90, 108, 183, 60, 65}.
a.1. Postulats
Le test qui suit demande plus de travail car il faut recoder les données brutes, pour ne retenir que la différence entre deux scores. Nommons Di = Xi – Yi. Nous obtenons alors un échantillon D composé de différences { Di }. Par la suite, on peut calculer la moyenne des
différences et la variabilité (non biaisée) dans les différences, ![]() et n−1
et n−1 ![]() . Bien que chaque différence ne soit pas forcément normalement distribuée, la moyenne l’est sans aucun doute, en vertu du théorème central limite (car la moyenne et la variabilité des différences doivent avoir une valeur spécifiable dans la population). On se retrouve donc à appliquer le même test qu’à la section 6.
. Bien que chaque différence ne soit pas forcément normalement distribuée, la moyenne l’est sans aucun doute, en vertu du théorème central limite (car la moyenne et la variabilité des différences doivent avoir une valeur spécifiable dans la population). On se retrouve donc à appliquer le même test qu’à la section 6.
La liste des différences est donnée par D = {2, -6, 2, 34, 21, -57, -1, -34, 5, -3, 48, 37, -11, -9, 34, -3, 28, 20, -46, 7, 74, 3, 27, -15, 2, 8, 2, 46, 3, 47, 59, 8, 12, 28, 51, -25, 4, 29, -27, 3}.
a.2. Hypothèses et seuil
L’hypothèse nulle précise que le Q. I. n’est pas affecté après la séquence d’entraînement (absence d’effet). Dans ce cas, la différence attendue entre avant et après devrait être de zéro. Dans l’expérience 3, on recherche un accroissement du Q. I., et donc un test unicaudal est utilisé. Le chercheur opte pour un seuil standard de 5%. Les hypothèses formelles sont :
H0 : ![]() = 0
= 0
H1 : ![]() > 0
> 0
a.3. Chercher le test
Le test est de la forme :

pour lequel la valeur  ~ t ( n – 1 ). Dans ce test, pour obtenir le degré de liberté permettant de savoir quelle forme la distribution de t utiliser, il faut soustraire 1 au nombre d’observations n (40 dans l’expérience 3). Après un regard dans la Table 5, on trouve une valeur critique s(α) égale à 1.686 (puisque le degré de liberté 39 n’est pas tabulé, utilisez le degré de liberté moins strict le plus proche, soit 38 ici).
~ t ( n – 1 ). Dans ce test, pour obtenir le degré de liberté permettant de savoir quelle forme la distribution de t utiliser, il faut soustraire 1 au nombre d’observations n (40 dans l’expérience 3). Après un regard dans la Table 5, on trouve une valeur critique s(α) égale à 1.686 (puisque le degré de liberté 39 n’est pas tabulé, utilisez le degré de liberté moins strict le plus proche, soit 38 ici).
Nous calculons la moyenne ![]() = 10.18, et l’écart type non biaisé n−1
= 10.18, et l’écart type non biaisé n−1 ![]() = 28.0. Le dénominateur est, comme toujours une erreur type dont la valeur est
= 28.0. Le dénominateur est, comme toujours une erreur type dont la valeur est ![]() = 4.42. Le résultat total est donc 2.30. Ce résultat étant nettement supérieur à la valeur critique, on conclue que la séquence d’entraînement dans l’expérience 3 résulte dans un accroissement significatif du quotient intellectuel. L’interprétation est : « L’amélioration des performances est significative (t(39) = 2.30, p < .05). Les sujets se sont améliorés en moyenne de 10.18 ».
= 4.42. Le résultat total est donc 2.30. Ce résultat étant nettement supérieur à la valeur critique, on conclue que la séquence d’entraînement dans l’expérience 3 résulte dans un accroissement significatif du quotient intellectuel. L’interprétation est : « L’amélioration des performances est significative (t(39) = 2.30, p < .05). Les sujets se sont améliorés en moyenne de 10.18 ».
Pour conclure, on note que la séquence d’entraînement semble belle et bien fonctionner. Les résultats étaient significatifs pour les expériences 1, 2 et 3. Cependant, dans l’expérience 1, le résultat obtenu n’inclut pas dans son intervalle de confiance la valeur 120, et dans l’expérience 3, l’accroissement est significativement inférieur à 20 points (faites le test avec l’hypothèse H0 : ![]() = 20). Le Pr Lear devrait donc réviser ses prétentions; il semble certain que l’entraînement accroît de 10 points, peut être plus, mais pas jusqu’à 20 points, le Q. I. de ceux qui le suive.
= 20). Le Pr Lear devrait donc réviser ses prétentions; il semble certain que l’entraînement accroît de 10 points, peut être plus, mais pas jusqu’à 20 points, le Q. I. de ceux qui le suive.
Biais et efficacité
Supposons une distribution D ayant un seul paramètre Ω: D(Ω). Un des buts de la statistique inductive est de déterminer la valeur de Ω. Par exemple, si la population est normale N(μ, σ), on veut une façon d’estimer μ (et aussi une façon d’estimer σ). Puisque la normale est symétrique, on peut utiliser aussi bien la médiane
que le mode
pour estimer le paramètre μ. Or pourquoi se fait-il que nous utilisons toujours
? L’intuition est que
est plus « efficace » pour estimer μ. Autrement dit, il faut moins de données dans notre échantillon pour obtenir un estimé de μ si on utilise la moyenne plutôt que la médiane ou le mode. Cette intuition, les statisticiens l’ont formalisé avec la notion de biais et d’efficacité.
Biais (def): Une statistique
est un estimateur sans biais du paramètre Ω si la valeur attendue de la statistique
est égale au paramètre Ω.. On note en abrégé E(
) = Ω. Imaginez que l’on collecte un grand nombre d’échantillon et que l’on moyenne toutes les statistiques ainsi collectée, est-ce que cette moyenne est proche de Ω ou s’en éloigne-t-elle systématiquement?
La moyenne
est un estimateur sans biais de μ. Un exemple de statistique biaisée est n X, la variance biaisée du paramètre σ. Nous avons dit au cours 2 que cet estimateur de σ est biaisé. Pour le démontrer, il suffit de montrer que E(n – 1 X2) ≠ Var(X). En voici la preuve:
On voit qu’en moyenne, la variance de l’échantillon est trop petite par un facteur (n-1)/n .
Efficacité (def): Une statistique
est un estimateur efficace d’un paramètre si la variance de cette statistique est minimale.
Par exemple, la médiane
et le mode
sont aussi des statistiques qui estime sans biais le paramètre μ d’une distribution normale N(μ, σ) puisque la normale est symétrique.
Cependant, le mode est extrêmement variable, et la médiane l’est aussi beaucoup, chose que l’on note: Var(
) >Var(
) > Var(
). Nous n’en ferons pas la preuve ici. Ce que signifie l’efficacité est que l’erreur type est moindre pour l’estimateur le plus efficace. Comme tous les tests statistiques sont basés sur une erreur type, la statistique qui a la plus petite erreur type donnera le test le plus puissant.
Exercices
1. Un échantillon comprend 40 participants et la somme des écarts à la moyenne au carré est de 404. Calculez l’erreur type.
2. Étant donné deux groupes indépendants avec respectivement 12 et 10 données brutes, quel est le degré de liberté pour réaliser un test comparant la moyenne des deux échantillons?
3.Étant donné les deux groupes de la question 2, quelle est la valeur critère s (α) si nous appliquons un test unicaudal avec α = 5%?
4.Quel est la valeur critère pour un test z unicaudal utilisant un seuil de :
a) 1%
b) 5%
c) 10%
5. Quel est la valeur critère pour un test z bicaudal utilisant un seuil de :
d) 1%
e) 5%
f) 10%
6. Un article mentionne deux groupes indépendants de participants dont les moyennes sont de 23.76 et 42.33. L’erreur type est de 2.58 et le degré de liberté est de 21. Combien de sujets cette étude comporte-t-elle au total?
7. Étant donnée les échantillons t indépendants suivants : ![]() = 21.08, n−1
= 21.08, n−1 ![]() = 3.66, nX = 13,
= 3.66, nX = 13, ![]() = 19.80, n−1
= 19.80, n−1![]() = 3.16, nY = 10,
= 3.16, nY = 10,
a) Calculer l’erreur type
b) Faites un test t
c) Trouver la valeur critique pour un seuil de 5%
d) Concluez
8. Un premier groupe a une moyenne de 5.5 et une variance non biaisée de 4.25. Le second groupe a une moyenne de 4.9 et une variance de 2.58. Au total, 42 participants ont été étudiés dans des groupes égaux. Faites le test approprié.
9. Si le degré de liberté d’un groupe unique est de 43 et la somme des écarts à la moyenne au carré de 1024, l’échantillon compte combien de sujets?
10. Une distribution de moyennes se distribue-t-elle de façon normale?
11. À partir des statistiques suivantes portantsurdeuxgroupes indépendants, faites le test statistique bicaudal approprié avec un seuil de 5% : Groupe 1 : moyenne 47, écart type 15.9, 23 sujets; Groupe 2 : moyenne 59, écart type 30.9, 27 sujets.
12. À partir des statistiques suivantes portant sur un groupe unique mesuré avant et après un traitement, faites le test bicaudal approprié avec un seuil de 5%: Avant : moyenne 107, écart type 15.9, 33 sujets; Après : moyenne 159, écart type 30.9, 27 sujets.
13. Soit une expérience à mesures répétées, où les données brutes sont, dans l’ordre des sujets Avant = {25, 23, 30, 7, 3, 22, 12, 30, 5, 14} et Après = {28, 19, 34, 10, 6, 26, 13, 47, 16, 9}. Les résultats sont-ils meilleurs après?
14. Dans la question 13, existe-t-il plus d’un test? Et si oui, lequel est le meilleur? Lequel est basé sur les postulats les plus
restrictifs (et donc plus à même de ne pas être satisfaits)?
15. Pour évaluer l’efficacité d’une nouvelle méthode didactique, le chercheur choisit un seuil de signification…
a) Permettant de concilier les deux risques d’erreur
b) Trèssévèrecarlesconséquencesde l’erreur α seraient catastrophiques
c) Très sévère car les conséquences de l’erreur β seraient catastrophiques
d) Trèspeusévèrecarlesconséquences de l’erreur β seraient catastrophiques.
16. Un échantillon de 25 mesures donne une moyenne de 218 et une somme des écarts à la moyenne au carré de 2400. Quelles sont les limites de l’intervalle de confiance, si le seuil de la recherche est de 5%.
17. Un échantillon de 2970 personnes mesurées lors d’un test de Stanford- Binet donne une moyenne de 102.1 et un écart type de 17.0. Est-ce que cet échantillon provient d’une population ayant un Q. I. de 100 (avec un seuil de 1%)?
18. On administre un test d’aptitude à 42 sujets de 10 ans. La moyenne est de 53.3. Si l’on postule que la population est normalement distribuée avec un écart type de 10, est-ce que la moyenne de la population peut être de 50?
19. Si le score z d’une donnée brute extraite d’un échantillon de 420 personnes est de 1.04 alors que la donnée non normalisée était de 65.6 et l’écart type non normalisée était de 15, quelle est la moyenne originale?
Si vous remarquez des informations erronées ou manquantes, merci de le partager par les Commentaires.





