C4: Statistiques inductives
Section 1. Le hasard comme une forme de déterminisme
On a coutume de penser qu’il existe un continuum allant du simple au complexe. Les phénomènes simples sont ceux qui sont parfaitement prévisibles, comme le levé du soleil, la réflexion de la lumière sur un miroir et les arcs réflexes. On appelle ces phénomènes des systèmes déterministes car les relations de causes à effets sont parfaitement bien identifiées et qu’aucun aléa n’entre en ligne de compte. À l’autre extrême, les phénomènes complexes regroupent les événements très difficiles, voir impossibles à prévoir. De bons exemples sont: la météo à moyen terme: pleuvra-t-il dans 14 jours? La turbulence dans l’écoulement d’un cours d’eau: la goutte de colorant rouge ira-t-elle à droite ou à gauche du rocher? Ces systèmes sont aussi appelés des systèmes chaotiques ou dynamiques.
Le summum d’un système complexe serait un système où il est impossible de prévoir le résultat. Par exemple, le lancer à pile ou face: il est impossible de prévoir le côté si le lancé est bien fait. Cependant, un paradoxe apparaît: les systèmes les plus imprévisibles sont aussi les plus prévisibles à longue échéance: Sur 10 000 lancés à pile ou face, vous aurez for probablement une proportion très proche de 5000 piles, ± 1 %. La précision est presque aussi grande que pour un système déterministe. Les distributions comme la binomiale B, la normal N ou la Weibull W sont en fait les lois du hasard.
Les systèmes les plus complexes ne sont pas les systèmes aléatoires. Ils se trouvent en fait à mi-chemin entre les systèmes déterministes et les systèmes chaotiques. La turbulence de l’eau n’est pas chaotique parce qu’on ne connaît pas les équations de l’écoulement de l’eau, au contraire, mais à cause du trop grand nombre de degré de liberté impliquée (chaque molécule). Le cerveau est l’exemple ultime d’un système dynamique: bien que le comportement des neurones soit relativement bien compris, nous sommes loin d’une théorie de l’esprit.
Section 2. Objectifs et méthodes de l’inférence statistique
2.1. L’objectif général de la méthode statistique
L’objectif de base de l’inférence statistique est de tester une idée que nous avons sur le monde. Que nous pensions que la terre tourne, que la matière est composée de Quark ou que l’esprit humain ne résulte que des neurones de nos cerveaux, il faut pour en avoir le cœur net procéder à toute une démarche formelle qui vérifiera ou invalidera notre intuition. Cette démarche formelle, qu’on appelle la démarche scientifique, est nécessaire parce que le monde est complexe, et par simple observation, il n’est pas possible de voir directement si nos intuitions sont vraies. Par exemple, Foucault a déterminé que si la terre tourne belle et bien, un gigantesque pendule devrait avoir des oscillations qui varient selon la latitude. Cette idée constitue une hypothèse formelle indiscutable. Par ailleurs, nous ne connaissons toujours pas comment démontrer si la matière est constituée de Quark. Cette idée scientifique ne conduit pas à des hypothèses qui puissent être confrontées avec la réalité.
À la base de la démarche, il faut premièrement mettre de l’ordre dans nos intuitions pour en arriver à des hypothèses formelles. Ces hypothèses formelles sont importantes pour enlever la part de subjectivité, la part d’interprétation libre. Par ailleurs, il faut aussi simplifier la complexité du monde en déterminant dans quel sous-ensemble de situations nous allons procéder à l’observation. Il s’agit de décider des conditions expérimentales dans lesquelles nous allons prélever un échantillon d’observation. Alors que la méthode statistique indique comment procéder à l’énoncé d’hypothèses formelles, la méthode scientifique aide à décider des conditions expérimentales. La Figure 1 montre la dichotomie entre les deux mondes.

La dernière étape est de confronter l’hypothèse de recherche avec l’échantillon. Seulement à cette dernière étape a-t-on une rencontre entre l’intuition et la réalité. Il faut alors décider: le monde observé est compatible avec notre intuition ou il ne l’est pas. La décision est toute ou rien, oui ou non.
2.2. Les objectifs spécifiques de la méthode statistique
Jusqu’à présent, nous avons vu en probabilité les lois qui indiquent comment se distribuent les valeurs dans une large population. Ces populations sont généralement spécifiées par un ou quelques paramètres, que ce soit μ et σ pour une population normalement distribuée, ou encore α, β, et γ pour les extrêmes d’une population (suivant la distribution de Weibull). Cependant, dans les faits, on peut avoir une idée de la forme de la distribution d’une population, mais certainement pas la valeur exacte de ses paramètres. Le travail du scientifique étant d’arriver à des assertions vraies et générales (portant sur la population entière) et non pas de faire des assertions vraies sur l’échantillon qu’il a obtenu, il doit pouvoir inférer à partir de son échantillon des vérités sur la population. La statistique inductive se charge de ce passage de l’échantillon à la population entière.
Le but de l’inférence statistique est d’inférer, à partir d’un échantillon, les valeurs probables des paramètres d’une population.
Les statistiques descriptives nous permettent de connaître les caractéristiques de notre échantillon. Il peut parfois être intéressant d’obtenir des informations sur un échantillon, mais la plupart du temps, on s’intéresse à un ensemble beaucoup plus large, la population entière. Puisque les populations sont souvent trop vastes pour qu’on puisse en mesurer directement les paramètres, on doit les estimer à partir des seules informations disponibles, celles qui proviennent d’échantillons.
L’échantillon tente de nous donner des informations sur la population (tel la moyenne et la variance), les vrais paramètres d’une population étant souvent inconnus. Peut-on conclure
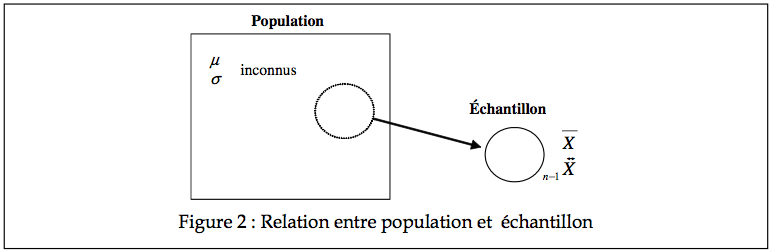
par exemple que la moyenne μ = ![]() la moyenne de notre échantillon? Jusqu’à quel point peut-on être confiant de cette inférence? Si quelqu’un d’autre affirme qu’en réalité, μ est un millième plus petit, est-t-il possible qu’il ait raison lui aussi? Si un autre encore affirme que μ devrait être de tant, peut-on le discréditer? La Figure 2 montre un échantillon provenant d’une population.
la moyenne de notre échantillon? Jusqu’à quel point peut-on être confiant de cette inférence? Si quelqu’un d’autre affirme qu’en réalité, μ est un millième plus petit, est-t-il possible qu’il ait raison lui aussi? Si un autre encore affirme que μ devrait être de tant, peut-on le discréditer? La Figure 2 montre un échantillon provenant d’une population.
Par exemple, en période électorale, les politiciens aimeraient bien connaître l’intention de vote de toute la population. Ils doivent pourtant se contenter des mesures prises par les maisons de sondage sur des échantillons limités.
Un autre exemple de statistiques inductives concerne les manipulations du chercheur (que ce soit un traitement ou autre). Pour savoir si un traitement a vraiment le potentiel d’aider les gens, on veut savoir si μT diffère de μR, toutes choses étant égales par ailleurs. Encore une fois, la seule source d’évidence que nous aillons est notre échantillon avec ses statistiques descriptives, tel ![]() et
et ![]() . Comme il est somme toute impossible que
. Comme il est somme toute impossible que ![]() soit exactement égal à
soit exactement égal à ![]() , quelle différence sommes nous prêt à accepter pour que les deux populations soient considérées comme différentes? À l’opposée, quelles différences sont jugées insignifiantes? Voir la Figure 3.
, quelle différence sommes nous prêt à accepter pour que les deux populations soient considérées comme différentes? À l’opposée, quelles différences sont jugées insignifiantes? Voir la Figure 3.

2.3. Méthodes des statistiques inductives
Pour bien faire les choses, il faut passer par quatre étapes.
a. Poser les hypothèses de travail
Les tests statistiques sont des tests d’hypothèses parce que leur application peut conduire au rejet de l’hypothèse nulle (H0). L’hypothèse nulle stipule toujours qu’il n’existe pas de différence à part les différences produites par le hasard de l’échantillonnage.
Des exemples d’hypothèses sont données par :
H0 : μ = μ0, où μ 0est une valeur précisée préalablement par une théorie.
H0 :μ1 = μ2 , où les μ réfèrent à des populations d’où sont extraits des échantillons différents.
H0 : F = F0, où F fait référence à la distribution (cumulative) d’une population, et F0 est une distribution précisée préalablement par le chercheur.
Les hypothèses peuvent être très variables, mais H0 postule toujours une absence de différence.
b. Choisir le seuil de confiance dans notre décision
Pour déterminer si la différence est significative (probablement pas due au hasard), il faut d’abord choisir un seuil qui définit le risque d’erreur qu’on est prêt à accepter. Ce seuil de signification définit la région de rejet de l’hypothèse nulle. Par convention, on utilise en général un seuil de 10%, 5% ou 1%. L’hypothèse nulle sera rejetée si la différence observée a une probabilité très faible de se produire par pur hasard (inférieur au seuil). Si l’hypothèse nulle est rejetée, l’hypothèse alternative (H1) est acceptée, ce qui veut dire qu’il est permis de penser que les deux échantillons proviennent de populations différentes. Les deux populations sont alors significativement différentes pour au moins un de leur paramètre. Comme il est impossible d’être toujours parfaitement confiant dans notre décision, nous choisissons à priori un seuil α de confiance (ex. 5%) tel que notre conclusion serait correcte 95% du temps, si seulement le hasard contamine notre échantillon. Nous verrons plus loin qu’il existe toujours un risque d’erreur dont il est important de tenir compte.
c. Chercher le test adéquat en fonction des hypothèses et du seuil
Il est nécessaire de connaître suffisamment la population pour pouvoir émettre des postulats. Est-elle une suite d’essai de Bernoulli? Est-elle distribuée normalement? Par souci de généralité, on va préférer des postulats très généraux, comme c’est le cas pour la plus haute marée annuelle, où le seul postulat nécessaire est que notre mesure est la plus grande marée observée dans toute l’année (auquel cas, la population des plus hautes marées se distribue comme une Weibull). Un autre exemple a lieu lorsque nous affirmons que notre variable est aléatoire à cause d’un grand nombre d’effets sous-jacents non observables individuellement. Nous postulons donc, grâce à l’approximation normale de la distribution binomiale, que les mesures sont normalement distribuées. Parfois, des approximations sont nécessaires comme lorsque l’on souhaite comparer des notes. Le professeur va postuler une distribution normale alors qu’il n’est pas claire pour un examen avec peu de questions que l’approximation normale de la binomiale est valide. Finalement, comme nous le verrons au cours 5, il y a des cas où des postulats sur la statistique plutôt que sur la population d’où est tirée cette statistique soit suffisants (par exemple, sur la distribution des moyennes ![]() ), peu importe la population d’origine.
), peu importe la population d’origine.
Bien identifier les postulats peut parfois être difficile, mais si on utilise un test alors que le postulat sous-jacent à ce test n’est pas satisfait, on se trouve à tirer des conclusions qui ne sont pas fondées.
Un test statistique n’est rien de plus qu’une recette qu’on applique. Il se formule toujours suivant une règle du genre : « Rejeter H0 si k > s(α) ». Dans cette formulation, k est une statistique (spécifiée par le test) qui peut être une statistique simple (comme ![]() ) ou plus complexe (comme G2 ou F). La façon d’obtenir la valeur critique est aussi spécifiée par le test, et dépend uniquement de notre seuil α choisi à priori (et non pas de l’échantillon) et du type de test. Un test bien fait garanti que la probabilité de rejeter H0 alors que H0 est vrai (dû à des fluctuations de l’échantillon) n’excède pas α ( Pr{ rejet H0 | H0 } ≤ α ). Bien entendu, ceci suppose que l’échantillon est représentatif, choisi sans biais, et que des contrôles sont en place. Ces derniers facteurs (facteurs externes à la méthode statistiques) ne peuvent pas être quantifiés par le test statistique et sont donc la responsabilité du chercheur (ce sont des facteurs liés à la méthode expérimentale).
) ou plus complexe (comme G2 ou F). La façon d’obtenir la valeur critique est aussi spécifiée par le test, et dépend uniquement de notre seuil α choisi à priori (et non pas de l’échantillon) et du type de test. Un test bien fait garanti que la probabilité de rejeter H0 alors que H0 est vrai (dû à des fluctuations de l’échantillon) n’excède pas α ( Pr{ rejet H0 | H0 } ≤ α ). Bien entendu, ceci suppose que l’échantillon est représentatif, choisi sans biais, et que des contrôles sont en place. Ces derniers facteurs (facteurs externes à la méthode statistiques) ne peuvent pas être quantifiés par le test statistique et sont donc la responsabilité du chercheur (ce sont des facteurs liés à la méthode expérimentale).
Autrement dit, nous voulons un test qui quantifie la probabilité d’obtenir une certaine différence par pur hasard. Si cette probabilité est faible, c’est à dire si cet événement est improbable, nous concluons que la différence est significative.
Une autre façon de voir la chose est d’imaginer la statistique k (par exemple, la moyenne) si nous pouvions répéter l’expérience un grand nombre de fois. Il est certain que d’un échantillon à l’autre, la statistique variera légèrement. En fait, nous pourrions faire la distribution de notre statistique. Sur la figure ci-contre, nous illustrons une distribution (quelconque) censée représenter la répartition des k après une infinité de réplication. Il arrivera bien quelques fois que k soit anormalement grand par pur hasard. En fait, si l’on fait effectivement ces nombreuses réplications, on pourrait trouver une valeur z tel que k ne l’excède pas dans 95% des situations. Dans ces cas, étant peu probable que k excède cette valeur par pur hasard, on est plus enclin à penser que k l’excède à cause de notre manipulation expérimentale. L’endroit où on coupe est la valeur critique, appelé ci-haut s ( α ).
Dans les faits, on ne répète pas une expérience un grand nombre de fois pour savoir où placer la valeur critique mais on se fie plutôt sur les postulats qui permettent d’établir la distribution théorique de k.
Les tests statistiques sont parfois distribués en deux catégories. Ce sont les tests paramétriques et les tests non-paramétriques. De façon superficielle, un test paramétrique permet de prendre une décision sur la valeur d’un paramètre d’une population. Par exemple, si notre population est une distribution normale (avec donc les paramètres μ et σ ), poser un diagnostic sur la valeur probable de μ exige un test paramétrique. Par contre, si l’on souhaite faire un test sur la médiane, puisque la médiane n’est pas un paramètre définissant une population normale, on pose alors un diagnostic non paramétrique à l’aide d’un test non paramétrique.

d. Appliquer le test et conclure
En suivant la recette identifiée lors du choix du test, le chercheur calcule à partir de son échantillon la bonne statistique k. Il trouve aussi (souvent à partir de tables) la valeur critique s(α). La conclusion découle de la comparaison entre la statistique empirique et la valeur critique.
2.4. Les risques d’erreurs
Lorsque nous portons un jugement sur l’hypothèse H0, il est facile de voir que cela comporte un risque. En fait, deux types d’erreurs sont possibles : L’erreur α (ou erreur de type I) et l’erreur β (ou l’erreur de type II).
L’erreur α est commise lorsque l’on rejette H0 alors qu’en réalité cette hypothèse est vraie. Elle est donc commise lorsqu’on croit que la différence observée découle d’une différence significative alors qu’elle est due au hasard. Cette erreur est heureusement quantifiable en terme de probabilité (grâce à nos postulats), puisqu’il s’agit du seuil de signification utilisé. Le chercheur décide donc lui-même du risque à prendre de commettre l’erreur α.
De même, il peut arriver de ne pas rejeter l’hypothèse nulle alors que cette hypothèse est fausse. Cette erreur est commise lorsqu’on croit que la différence observée (étant faible) est due au hasard alors qu’en fait elle résulte de différences dans les populations. Il s’agit alors d’une erreur β.

Les erreurs α et β sont étroitement liées. Ainsi, moins le seuil de signification α est sévère (i.e. un seuil à 10% plutôt qu’à 5%) plus il est risqué de commettre l’erreur α. Inversement, plus le seuil est sévère (i.e. un seuil à 1% plutôt que 5%), plus on risque de commettre l’erreur β.
On illustre sur la Figure 5 cet espèce de trade-off entre l’erreur α et β. La distribution de gauche donne la distribution de notre statistique si l’hypothèse H0 est vraie. La distribution de droite donne la distribution de k si H0 n’est pas vraie. La ligne verticale représente la position de notre valeur critique. La zone hachurée indique le fait que notre statistique k peut parfois être petite (par pur hasard) quand H0 est faux, si petite en fait qu’elle sera inférieure à notre valeur critique. Dans ce cas, on croira que k est probablement le résultat d’une population où H0 est vrai, de façon erronée (erreur β). De même, il peut arriver que sous H0, k soit particulièrement élevé, laissant croire qu’il résulte probablement d’une différence réelle, et non pas du simple hasard (erreur α). Si l’on choisit un seuil α plus sévère (par exemple 1% au lieu de 5%), on se trouve à déplacer la valeur critique s ( α ) vers la droite (et la zone grise aura une surface de 1%). On risque alors de faire moins d’erreur α (car il est encore moins probable que k excède la valeur critique par pur hasard) mais la probabilité de faire une erreur β s’accroît (quand H1 est vrai, k n’a pas besoin d’être aussi petit pour excéder s ( α ) si on le déplace vers la droite). Tout l’argument s’inverse si l’on choisit un α moins sévère (10% au lieu de 5% par exemple).

Alors que l’on connaît la probabilité de faire l’erreur α, il est difficile de quantifier la probabilité de faire l’erreur β. En effet, on peut préciser la distribution théorique de k sous H0 car l’hypothèse nulle spécifie une situation précise. Par contre, l’hypothèse alternative est vague, d’où l’impossibilité d’établir avec précision la distribution des valeurs de k quand H1 est vrai. Nous verrons à la fin du cours des heuristiques pour quantifier la probabilité d’une erreur β et en réduire le risque.
Lors de la planification d’un test statistique (étape b), le seuil de signification est établi en fonction des conséquences possible de l’une ou l’autre de ces deux erreurs. Si le rejet de l’hypothèse nulle, lorsqu’elle est vraie, cause un résultat catastrophique, la valeur α doit être relativement petite (plutôt 0.01). D’autre part, si le non-rejet de l’hypothèse nulle, alors qu’elle est vraie, entraîne une plus grande catastrophe, il faut choisir un seuil de signification moins sévère (disons 0.10).
Il arrive qu’il soit plus grave de commettre une de ces deux erreurs que l’autre, mais en général, l’impact de l’une ou l’autre de ces erreurs est tout aussi important. Il s’agit d’essayer de concilier les deux risques. C’est généralement le cas en psychologie où les seuils choisis varient entre 0.05 et 0.01. Voici un exemple où l’on doit concilier les deux sources d’erreurs.
Une compagnie pharmaceutique produit un médicament destiné à guérir un certain type de cancer. Ce médicament semble efficace mais comporte certains effets secondaires. La compagnie veut donc vérifier statistiquement si ce médicament permet vraiment d’arrêter la maladie (H0 : le médicament n’a pas d’effet). Dans ce cas, si le seuil est trop élevé (disons 0.10), il existe un risque de commettre l’erreur α en rejetant H0 alors qu’elle est vraie. Une telle erreur amènera inutilement des malaises aux patients qui utiliseront ce médicament alors qu’il est inefficace. Par ailleurs, si le seuil de signification est trop sévère (0.001), il y a risque de ne pas rejeter H0 alors qu’elle est fausse et de commettre l’erreur β. On croira à tort que le médicament est inefficace alors que des personnes auraient pu être soignées.
Test unidirectionel vs. unicaudal
Deux autres façons de caractériser un test statistique est de dire (a) s’il est unidirectionnel ou bidirectionnel et (b) s’il est unicaudal ou bicaudal. Ces distinctions ne sont pas très importantes mais peuvent parfois aider à la compréhension. D’emblée, il faut dire que (a) n’est pas synonyme de (b).
(a) unidirectionnel vs. bidirectionnel
Cette distinction repose sur l’hypothèse alternative que nous opposons à H0. Souvent, nous voulons seulement savoir s’il existe une différence (et nous notons H1 en utilisant le signe ≠). Parfois, nous avons une hypothèse alternative plus précise qui spécifie que si différence il y a, elle ne peut être que positive (ou négative) et alors H1 utilise le signe > (ou <). Dans le premier cas, on appelle le test un test bidirectionnel et dans le premier, un test unidirectionnel (soit plus petit, soit plus grand).
(b) unicaudal vs. bicaudal
Ces termes indiquent quelle(s) extrémité(s) de la distribution est utilisée pour rejeter H0. En effet, pour certains tests, la distribution est symétrique et des valeurs très petites et très grandes sont toutes deux jugées suspectes. Pour d’autres distributions, seul des grandes valeurs sont suspectes et mènent au rejet de H0. C’est le cas de la distribution χ2 et F: puisque l’on met les termes au carré, il n’existe plus de différences négatives et une valeur basse (proche de zéro) signifie que H0 n’est pas rejetée. Dans ces deux cas, le test ne peut qu’être bidirectionnel quoique utilisant uniquement l’extrémité de droite de la distribution (unicaudal). De façon générale, un test bicaudal est forcément bidirectionnel mais un test unicaudal peut être aussi bien unidirectionnel que bidirectionnel.
Dans un test bicaudal, il faut deux seuils, un à droite et un à gauche de la distribution théorique, comme on le voit à la Figure 6. La probabilité de rejeter H0 doit être également répartie de chaque côté dans le cas d’un test bicaudal, d’où la valeur critique doit être choisie en fonction de α / 2.
Section 3.Tests utilisant la distribution binomiale
Nous présentons dans cette section trois tests, tous reliés à la distribution binomiale. Le premier permet de décider si une proportion observée est différente ou non d’une valeur pré- spécifiée. Les deux tests suivants sont des extensions du test binomial à la médiane et à des mesures du genre avant-après.
3.1. Test sur une proportion
Soit un chercheur souhaitant tester la proportion de personnes souffrant du syndrome de Bezières, un syndrome anodin, n’affichant aucun symptôme (et fictif) et pour lequel les gens vont rarement consulter. Suite aux recherches sur le génome humain, ce chercheur note que si le modèle standard de transmission des gènes est vrai, ce syndrome devrait être présent chez un quart de la population. Il procède donc à une première expérience, un test de dépistage génétique préliminaire sur un échantillon de 20 humains. Il observe 3 cas de syndrome de Bezières. Est-ce un résultat en faveur du modèle standard?
Ce qu’il faut ici, c’est un test de proportion, un test qui pourra nous dire si 3 sur 20 (15%) est significativement plus petit que 25%.
a. idée générale du test
Dans cette première expérience, le chercheur note le nombre de personnes qui souffrent du syndrome de Bezières en terme de« Succès » ou d’« Échec », c’est à dire, ayant ou n’ayant pas le syndrome. Le nombre total d’observations est noté n et le nombre de succès m. Puisqu’il s’agit d’essais de Bernoulli, l’hypothèse que la proportion est de 1⁄4 permet de tracer le graphe des histogrammes du nombre de succès attendu, dans ce cas-ci, une B(20, 1⁄4):

Comme on le voit à la Figure 7, il est toujours possible, sur 20 essais de Bernoulli, d’obtenir 0 succès, mais la probabilité est petite (un coup d’œil à la Table 1 donne une probabilité d’environ 3 chances sur 1 000, moins de 1%). De la même façon, la probabilité d’avoir 14, 15, etc. succès est totalement négligeable (les probabilités sont de moins de 1 pour 10 000). Ces valeurs extrêmes sont excessivement non plausibles. Si on observe un nombre de succès dans ces zones, comme c’est trop improbable pour être le simple résultat du hasard (erreur d’échantillonnage), on conclue que la proportion de 1⁄4 ne doit pas être vraie dans la population entière.

On peut donc établir deux frontières (dans le cas d’un test bicaudal) pour lesquelles, si la valeur observée en fait partie, on jugera l’hypothèse non plausible. Voir Figure 8.. Ces deux frontières délimitent ce qu’on appelle la zone de rejet; la position des frontières est données par s – et s+. Il est important de répartir de chaque côté la moitié de notre seuil α. En utilisant la Table 1, on calcule pour quels histogrammes la probabilité d’obtenir une valeur au delà vaut α / 2 (ou est le plus proche de α / 2 sans l’excéder).
b. Structure du test
b.1. Postulat
Ce test est basé sur le postulat que chaque essai est un essai de Bernoulli, c’est à dire qu’il ne peut y avoir que deux résultats: succès ou échec pour chaque mesure. On note par n le nombre total d’observations et par m le nombre de succès.
b.2. Hypothèses et seuil
L’hypothèse nulle est que la population montre une proportion p0 de gens souffrant de ce syndrome, cette valeur étant déduite des travaux du chercheur. L’hypothèse alternative est soit (unidirectionnel) (a) la proportion réelle dans la population est plus grande, (b) la proportion réelle est plus faible, ou (bidirectionnel) (c) la proportion est différente, plus grande ou plus basse. Dans le cas (c), le test est dit bicaudal puisqu’il teste la possibilité de différences à un ou l’autre bout de la distribution. Autrement dit, on rejette H0 si la statistique observée m est supérieure, inférieur ou supérieure ou inférieur à une valeur critique. On note, selon le cas H0 : p = p0, et (a) H1: p > p0 , (b) H1: p < p0 ou (c) H1: p ≠ p0.
La valeur p0 est une constante précisée par le chercheur selon des considérations théoriques seulement. Le choix de l’hypothèse alternative (unidirectionnel ou bidirectionnel) dépend aussi de considérations à priori. Dans notre exemple sur le syndrome de Bezières, si le modèle standard est faux, n’importe quelle proportion est possible, le chercheur opte donc pour un test bidirectionnel:
H0 : p = 1⁄4
H1: p ≠ 1⁄4
Concernant le seuil, puisqu’il n’y a pas de vies en jeu, et que l’expérience met en jeu des techniques de manipulation génétique assez routinière, il n’y a pas lieu de choisir un seuil très élevé ou très bas. Il choisi le seuil standard α = 0.05.
b.3. Chercher le test
Le test est de la forme :

pour lequel la valeur m ~ B(n, p0 ). Notez qu’ici, le test utilise ≤ et ≥ plutôt que < et > car la frontière est incluse dans la zone de rejet. Après un examen dans une table B(20, 1⁄4 ), le chercheur trouve d’un côté que la probabilité d’obtenir 0 ou 1 succès est de 2.43% alors que la probabilité de 0, 1 ou 2 succès excède α / 2. De l’autre côté, la probabilité d’obtenir 10 succès ou plus est de 1.39% (0.0099 + 0.0030 + 0.0008 + 0.0002 + 0.0000) alors que la probabilité de 9 succès ou plus excède α / 2. La zone de rejet est donc à droite [0..1] et à gauche, [10..20]. Les frontières sont s -(α / 2) = 1 et s+(α / 2) = 10.
b.4. Appliquer le test et conclure
Le test est facile, puisque la seule statistique nécessaire est le nombre de succès m. Nous avons vu que m = 3, qui n’est pas dans une ou l’autre zone de rejet. Le chercheur conclu que les résultats obtenus ne remettent pas en cause le modèle standard (non rejet de H0).
3.2. Test non paramétrique sur la médiane
La plupart des tests du cours 5 et suivants sont des tests sur la moyenne. Cependant, il arrive des situations où la population d’où provient l’échantillon a une distribution très asymétrique. Dans ce cas, les postulats à la base de ces tests sont invalidés. Une alternative est d’utiliser le test sur la médiane qui suit. Ce test n’est pas aussi puissant, mais il est valable peu importe la population de base. Un exemple de population problématique pour un test de moyenne est le revenu annuel. En effet, dans la population nord-américaine, le revenu est en général assez faible (de l’ordre de 20 à 40 K$). Cependant, il existe une petite quantité de millionnaire, et aussi des milliardaires. Pour un milliardaire et mille personnes avec un revenu de 10 K$, le revenu moyen est supérieur à 1 000 000 $! Dans ce contexte, la moyenne comme estimateur de la tendance centrale est loin de représenter la tendance centrale telle que je la vois…
Un test sur la médiane peut mieux cerner le revenue des Canadiens. Par exemple, supposons que le revenu médian lors du dernier recensement pan-canadien en 1996 ait été mesuré à 24 500 $ (chiffre fictif). Il ne s’agit pas d’une statistique puisqu’un recensement

mesure la population en entier. Le chercheur veut savoir si le revenu médian est à la baisse. Bien entendu, ce chercheur de l’université de Montréal ne peut pas se payer un recensement exhaustif. Il va donc procéder à un échantillonnage. Il observe sur un échantillon de 11 répondants, 2 personnes ayant un revenu supérieur au revenu médian de l’année 1996. Appelons cette statistique m, le nombre de « succès ». Ici, l’étiquette « succès » est arbitraire, mais permet de catégoriser les observations en deux classes: « supérieur à 24 500$ » ou « inférieur à 24 500$ ».
a. idée générale du test
L’idée fondamentale vient du fait que la médiane, par définition, partage les observations en deux classes de tailles égales. Ainsi, 50% des revenues de l’échantillon devraient être supérieurs à la médiane et 50% inférieurs. Il est donc possible de prendre l’échantillon X et pour chaque valeur qui est supérieure à la médiane hypothétique avancée par le chercheur, compter un succès. Notons par m le nombre total de succès. La suite du test est identique à un test sur une proportion sauf que la proportion attendue de succès est toujours de 1⁄2. Dans le paragraphe qui suit, nous présentons une autre façon de voir le test.
Une particularité de la distribution binomiale quand p = 1⁄2 est qu’elle est parfaitement symétrique. De ce fait, s’il y a deux histogrammes dans la zone de rejet à gauche pour couvrir une probabilité de rejet de α / 2, il faudra deux histogrammes à droite aussi, et la distance entre la valeur attendue, n / 2 et les zones de rejet sera la même (la distance | n / 2 – s+(α / 2) | = | n / 2 – s -(α / 2) | ). Appelons cette distance d(α / 2). Si H0 est vraie, m devrait être à peu près n / 2 et m – n / 2 devrait être à peu près zéro. On peut donc conduire le test de la médiane de deux façons: (a) comme avant en trouvant la zone de rejet et en regardant si m ∈ zone de rejet ou (b) en calculant la distance entre n / 2 et la zone de rejet, qu’on appelle la distance critique, puis en regardant si la distance m – n / 2 est supérieure à la distance critique. La méthode (a) entraîne moins de confusion, mais la méthode (b) sera généralisée dans la section suivante.
b. Structure du test
b.1. Postulats
Le test de la médiane est basé sur les postulats que chaque essai est un essai de Bernoulli. Chaque observation est notée un succès si elle excède la médiane de l’hypothèse ou un échec si elle est inférieure. Le p0 attendu est 1⁄2, bien entendu.
b.2. Hypothèses et seuil
L’hypothèse nulle est que la médiane de la population (appelons-la M) est de M0, une valeur établie par le chercheur à priori. L’hypothèse alternative est que soit (unidirectionnel) (a) la médiane réelle dans la population d’où provient X est plus grande que M0, (b) la médiane réelle dans la population d’où provient X est plus faible, ou (bidirectionnel) (c) la médiane dans la population d’où provient X est différente (plus grande ou plus basse). Dans le cas (c), le test est bicaudal. Si la médiane de l’échantillon est bien de M0, nous aurons un total de n / 2 succès. Si le nombre réel de succès s’écarte significativement de n / 2, nous pouvons rejeter l’hypothèse H0.
Autrement dit, on rejette H0 si (a)m-n/2>d(α), (b) m-n/2<-d(α),ou encore, dans le test bicaudal (c) si | m – n / 2 | > d (α/2). Dans le dernier cas, on utilise la valeur absolue entre n / 2 et m car il importe que la distance soit négative ou positive. On note, selon le cas
H0: M = M0, et (a) H1: M > M0 , (b) H1 : M < M0 ou (c) H1 : M ≠ M0 . Le choix de l’hypothèse alternative dépend du contexte de la recherche. Dans notre exemple ci-haut, le chercheur pense spécifiquement à une baisse du revenu. Il postule donc les hypothèses:
H0 : M = M0 H1: M < M0
On opte à nouveau pour le standard α = 0.05. Dans notre exemple sur les revenus, M0 est de 24 500 $.
b.3. Chercher le test
Le test est de la forme :
Rejet de H0 si m − (n/2) ≤ −d(α)
pour lequel la valeur m ~ B(n, 1⁄2 ). Après un examen dans une table B(11, 1⁄2 ), on trouve que la probabilité d’obtenir 0, 1, ou 2 succès sur 11 mesures est de 0.0005 + 0.0054 + 0.0269 soit 3.28%. La probabilité d’obtenir 3 succès ou moins est de 11.3%, supérieure à notre seuil de confiance et donc trop fréquente par pur hasard. La frontière se situe donc à s -(α) = 2. La distance critique d(α) est la distance entre n / 2 et la plus petite valeur permise telle que la probabilité soit ≤ α (i.e. n / 2 – s–(α) ). Donc, d(α) = 3.5 (la distance entre n / 2 = 5.5 et 2) pour laquelle pas plus de 5% de la distribution est située au-dessus par pur hasard.
b.4. Appliquer le test et conclure
Le calcul est plutôt simple dans ce cas, tout ayant été fait lors de la compilation des données. Nous avons m = 2 qui fait partie de la zone de rejet. En terme de distance, m – n / 2 = -3.5 qui est égale à -d(α) = -3.5. Dans les deux versions, on rejette l’hypothèse H0. Le revenu médian est inférieur à ce qu’il était lors du dernier recensement. On peut rajouter que dans ce cas-ci, l’échantillon est petit, et vu le faible coût lié à ce type de sondage, le chercheur aurait pu rechercher un échantillon plus large. Néanmoins, la méthode statistique est sans faille, et la probabilité d’obtenir aussi peu de répondants avec un revenu supérieur à 24 500 $ ne peut pas être le résultat du simple hasard.
Remarquez dans ce cas-ci que si le chercheur avait eu une hypothèse de travail plus vague (soit que le revenu médian a changé, sans avoir d’hypothèse sur la direction du changement), on se serait retrouvé avec un test beaucoup moins puissant. En effet, le test devenant bicaudal, la valeur critique doit tenir compte des deux extrêmes à la fois (répartir α / 2 à droite et α / 2 à gauche). Or, la probabilité d’obtenir 0 ou 11, 1 ou 10 ou 2 ou 9 succès est de 6.56% soit trop élevée pour notre seuil choisi à priori. La zone critique devient soit inférieure ou égal à 1 (s–(α / 2) = 1) ou supérieure ou égal à 10 (s+(α / 2) = 10). Comme on le voit, m n’est pas dans la zone critique. Alternativement, la distance critique d(α) entre n / 2 et s –(α / 2) est de 4.5. Or | m –11 / 2 | = -3.5 qui n’est pas plus petit que -4.5. Dans ces deux versions du test, on ne peut pas rejeter l’hypothèse H0. Ceci montre l’importance d’avoir une hypothèse alternative la plus spécifique possible étant donné le contexte de recherche, à défaut de quoi on perd de la puissance décisionnelle.
Comme l’illustre très bien cet exemple, l’hypothèse de recherche porte sur la médiane de la population (M) et pourtant notre test porte sur une statistique extraite de l’échantillon (m). Il en est toujours ainsi en statistique inductive. Remarquez aussi que la statistique retenue m n’a rien à voir avec une médiane. Il s’agit d’un nombre entier entre 0 et n, soit le nombre de valeur excédant la médiane hypothétique (M0). Nous n’avons aucune connaissance sur la répartition des revenus, cependant nous avons des informations sur la façon dont se répartissent les revenus par rapport à une médiane (comme un essai de Bernoulli).
Pour terminer, une petite question. Que doit-on faire si on obtient une observation Xi exactement égale à la médiane hypothétique M0? Doit-on compter un succès ou pas? Rappelez-vous que chaque essai doit être un essai de Bernoulli.
3.3. Test non paramétrique sur observations couplées
Le dernier test que nous présentons dans cette section concerne des observations couplées. Supposons que nous voulons tester une thérapie pour soigner les traumatismes psychologiques consécutifs à un diagnostic positif du syndrome de Bezières. Le chercheur songe à une thérapie béhavioriste. Cependant, pour bien vérifier qu’elle fonctionne, et étant donnée que l’éthique interdit de donner un traitement placebo à la moitié des patients, le chercheur décide de procéder à une mesure traumatique avant la thérapie béhavioriste et une seconde mesure après la thérapie. Si amélioration il y a, le chercheur va l’imputer à son traitement.
a. Idée du test
Une méthode simple pour tester le recouvrement des patients serait de regarder la différence avant-après dans leur manifestation morbide. Cependant, nous n’allons pas explorer cette idée avant le cours 5 car elle nécessite des postulats forts sur la différence entre deux scores. Supposons plutôt que nous n’avons aucune idée comment se répartissent les scores de morbidité. Bien entendu, il est fort improbable qu’un sujet score exactement pareil avant et après. Plus probablement, il va –si le traitement est inefficace- obtenir à peu près le même score, soit un peut plus ou un peu moins. Or, sur l’ensemble des sujets, certains seront un peu plus hauts après qu’avant alors que d’autres seront un peu plus bas après qu’avant. Dans l’ensemble, si le traitement est inopérant, on s’attend à ce que la moitié des patients soient plus hauts après. Voici ce qui peut nous servir de base pour un test. Pour chaque patient, notons un succès si son score de morbidité est supérieur après, un échec sinon. Chaque patient est donc un essai de Bernoulli, et un test binomial est parfaitement approprié. On appelle souvent ce test un test des signes car les statisticiens avaient coutume de mettre un « + » pour les scores qui se sont améliorés et un « – » pour les score qui ont diminués.
b. Structure du test
b.1. Postulat
Le test est basé sur le postulat que chaque observation est un essai de Bernoulli avec p = 1⁄2. Chaque observation est codée en terme de succès (amélioration suite au traitement) ou d’échec (réduction suite au traitement). Le nombre total de succès est noté m.
b.2. Hypothèses et seuil
L’hypothèse nulle est que la population avant, avec un taux de morbidité M1 n’a pas changée après la thérapie, et donc que sont taux de morbidité après (appelons-le M2) est identique. L’hypothèse alternative est que soit (unidirectionnel) (a) le taux a baissé dans la population traitée, (b) le taux a augmenté ou (bidirectionnel) (c) le taux est différent, plus grand ou plus bas. Dans le cas (c), le test est dit bicaudal. Si la population est bien la même, nous aurons n / 2 succès. Si le nombre réel de succès s’écarte significativement de n / 2, nous pouvons rejeter l’hypothèse H0. Dans ce cas-ci, on peut rejeter H0 si (a) m – n / 2 > d(α), (b)
m – n / 2 < -d(α), ou encore, dans le test bicaudal (c) si | m – n / 2 | > d(α). On note, selon le cas H0 : M1 = M2, et (a) H1: M1 > M2, (b) H1: M1 < M2 ou (c) H1: M1 ≠ M2. Le choix de l’hypothèse alternative dépend du contexte théorique. Dans notre exemple ci-haut, le chercheur pense spécifiquement à une baisse de la morbidité. Il postule donc les hypothèses:
H0: M1 =M2
H1: M1 > M2
Le chercheur opte pour un α = 0.10 puisque la thérapie est très exploratoire, et qu’il ne prétend pas avoir la thérapie parfaite du premier coup. Il veut plutôt une indication que la piste peut être prometteuse.
b.3. Chercher le test
Le test est de la forme :
Rejet de H0 si m − (n/2) ≥ d(α)
pour lequel la valeur m ~ B(n, 1⁄2). Notre chercheur ayant 10 patients, il note qu’après la thérapie, trois patients seulement montrent un score de morbidité supérieur au score précédent la thérapie. Après un examen dans une table B(10, 1⁄2), on trouve que la probabilité d’obtenir 0, 1, ou 2 succès est de 0.0010 + 0.0098 + 0.0439 soit 5.47%. La zone de rejet est [0..2]. La distance critique d(α) est de 3 (car n / 2 – s –(α) = 5 – 2 = 3) pour laquelle pas plus de 10% de la distribution est située au-dessus par pur hasard.
b.4. Appliquer le test et conclure
Le calcul est plutôt simple dans ce cas, tout ayant été fait lors de la compilation des données. Nous avons m = 3 qui n’est pas dans la zone de rejet [0..2]. Autrement dit, la distance m – n / 2 = 5 – 3 = 2 n’est pas plus grand ou égale à la distance critique d(α) = 3. On ne rejette donc pas l’hypothèse H0. La thérapie n’a pas réduit l’incidence des comportements morbides chez les traumatisés de Bezières.
Imaginons plutôt que le chercheur eut 20 patients au lieu de 10, et que 6 se soient améliorés après le traitement (exactement la même proportion que précédemment). Dans ce cas, la probabilité d’avoir 6 succès ou moins est de 0.0000 + 0.0000 + 0.0002 + 0.0011 + 0.0046 + 0.0148 + 0.0370 = 5.77%, inférieur à α. La valeur critique s -(α) est donc 6 (c’est à dire que la zone de rejet va de 0 à 6 inclusivement), et la distance critique est 4 (car n / 2 – 6 = 4). m étant dans la zone de rejet, l’hypothèse H0 est rejetée. De la même façon, m – n / 2 est égal à la distance critique 4, d’où rejet de H0. La thérapie a significativement réduit l’incidence des comportements morbides chez ces traumatisés.
Le fait d’accroître n a permis de rendre une décision différente. Est-ce signe que les statistiques sont inconséquentes? Non. Remarquez que puisque le chercheur ne peut pas considérer des demi-succès (ce sont des essais de Bernoulli), il est obligé d’arrondir son seuil pour accommoder le plus proche nombre entier de succès. Pour le test avec 10 patients, le seuil le plus élevé qui ne dépassait pas 10% était de 5.47%. En passant de 10 à 20, les choses étaient légèrement mieux, puisque la valeur critique entière la plus proche donnait un seuil de 5.77%. La différence dans les différentes décisions tient donc compte du fait que le nombre de patient doit être un nombre entier. Plus le nombre total de patient est grand, plus on peut avoir un seuil de décision qui soit proche de notre valeur α choisie à priori.
L’important est donc d’avoir autant de sujets que possible. Surtout qu’ici, la thérapie n’était pas miraculeuse : elle réduisait l’incidence des comportements morbides, mais ne les éliminait pas complètement. Il s’agit de la règle d’or : Plus la différence attendue est petite, plus il faut compenser avec beaucoup de sujets pour qu’elle puisse devenir significative. Nous reviendrons sur la puissance d’un test au cours 13.
Le travail de l’analyse statistique
L’écriture d’un rapport de recherche (ou d’un projet, au début de la maîtrise) peut sembler une aventure linéaire. Il n’en est rien. Le processus d’écriture scientifique est rempli de détour (parfois de retour en arrière). De plus, on peut penser que tout doit être rapporté dans le rapport. Une fois encore, il n’en est rien. Les postulats, les hypothèses formelles, et la valeur critique, entre autre, ne sont absolument pas présentés dans la méthodologie ni dans la section résultats. Ce sont des balises que se donne le chercheur pour bien remplir son travail. Cependant, le lecteur expérimenté (le réviseur?) va essayer de déduire vos hypothèses de votre écriture. Gare à vous si vous ne donnez pas assez d’information pour qu’il y arrive!
Section 4. Tests utilisant l’approximation normale de la binomiale
Dans le cours 3, j’ai indiqué que l’approximation normale de la binomiale tient si p0 est relativement près de 1⁄2 (pour avoir une distribution à peu près symétrique). Dans la pratique, l’approximation est valable si n p0 excède 10 et n est supérieur à 20. Ainsi, si la proportion prédite est faible, compensez en accroissant le nombre d’observation. Les tests présentés ici sont basés sur 2 postulats supplémentaires pour valider l’usage de l’approximation normale et concernent la taille de la population : n >> (i.e. supérieur à 20) et n p0 > 10 où p0 dépend de votre hypothèse à priori.
4.1. Test sur une proportion
Une façon simple de réaliser un test de proportion vient de la façon de coder nos résultats. Chacune des mesures individuelles est soit un succès ou un échec (par exemple, il possède le syndrome de Bezières ou non). Dans ce test, plutôt que de coder les observations en terme « Échec » ou « Succès », on va plutôt les noter en utilisant les chiffres 0 ou 1.
a. idée générale du test
Dans le cas où les données sont codées avec des zéros et des uns, une intéressante propriété apparaît : la moyenne des données reflète la proportion d’observer un succès.
Pour continuer l’exemple sur le syndrome de Bezières, supposons que le chercheur, insatisfait des résultats de l’expérience 1, procède à une expérience 2 avec cette fois-ci 1000 participants. S’il observe, disons, 250 cas de syndrome dans notre échantillon, la somme de 250 uns et de 750 zéros donne un total de 250, que l’on divise par n pour obtenir la moyenne, soit 0.25. Il s’agit de la proportion estimée d’obtenir, lors d’un essai, un individu ayant le syndrome.
Ceci se démontre facilement en terme mathématique en notant que
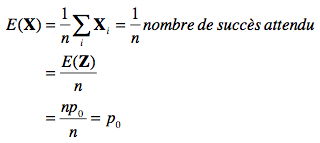
où Z est une variable aléatoire décrivant le nombre de succès attendus lors de n essais de Bernoulli. Nous avons que Z ~ B(n, p0), d’où la moyenne de Z, E(Z) = n p0, comme nous l’avons vu au cours 3.
De même, on trouve la variance de X en notant que
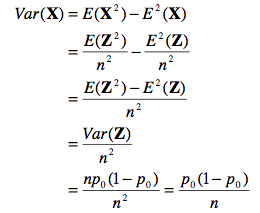
C’est donc dire que plus notre échantillon est grand, plus petite est la variance de notre moyenne autour de la proportion réelle. Donc, plus n est grand, plus nous sommes certains que notre estimé ![]() est proche de la vraie proportion p qui définie la population. Ceci est un très fort incitatif à utiliser de grands échantillons. La dernière étape est donc de voir que la différence entre la vraie proportion p0 et la proportion observée
est proche de la vraie proportion p qui définie la population. Ceci est un très fort incitatif à utiliser de grands échantillons. La dernière étape est donc de voir que la différence entre la vraie proportion p0 et la proportion observée ![]() doit être approximativement zéro, et ce avec une variance p0 (1 – p0) / n. Si l’on normalise,
doit être approximativement zéro, et ce avec une variance p0 (1 – p0) / n. Si l’on normalise,

on obtient donc, pour n >>, une variable normalement distribuée (approximation normale de la binomiale) avec une moyenne de zéro et un écart type de un (à cause de la normalisation). Nous avons les éléments pour faire un test statistique.
b. Structure du test
b.1. Postulats
Ce test est basé sur les postulats que chaque essai est un essai de Bernoulli et que le nombre d’observations est élevé (c. à d. n p > 10 et n > 20). Chaque observation est codée en zéro ou en un.
b.2. Hypothèses et seuil
L’hypothèse nulle est que la population montre une proportion p0 = 1⁄4 de gens souffrant du syndrome de Bezières, cette valeur étant déduite des travaux du chercheur. L’hypothèse alternative est que soit (unidirectionnel) (a) la proportion réelle dans la population est plus grande, (b) la proportion réelle est plus faible, ou (c) la proportion est différente, plus grande ou plus basse. Dans le cas (c), le test est dit bicaudal puisqu’il teste la possibilité de différences
à un ou l’autre bout de la distribution de ![]() . Autrement dit, on rejette H0 si notre statistique est supérieure à une valeur critique supérieure ou inférieur à une valeur critique inférieur. Comme la distribution normale standardisée est symétrique autour de zéro, les valeurs critiques sont les mêmes à un signe près (s+(α) = – s –(α) ) et que puisque
. Autrement dit, on rejette H0 si notre statistique est supérieure à une valeur critique supérieure ou inférieur à une valeur critique inférieur. Comme la distribution normale standardisée est symétrique autour de zéro, les valeurs critiques sont les mêmes à un signe près (s+(α) = – s –(α) ) et que puisque ![]() -p0 est zéro sous H0, la distance critique a la même valeur que s(α).
-p0 est zéro sous H0, la distance critique a la même valeur que s(α).
On note, selon le cas H0: p = p0, et (a) H1: p > p0 , (b) H1: p < p0 ou (c) H1: p ≠ p0. La valeur p0 est une constante précisée par le chercheur selon des considérations théoriques seulement, soit 1⁄4 dans notre exemple. Le choix de l’hypothèse alternative dépend aussi du contexte théorique. Dans notre exemple sur le syndrome de Bezières, si le modèle standard n’est pas vrai, toutes les relations sont possibles, on opte donc pour :
H0 : p = 1⁄4
H1: p ≠ 1⁄4
Concernant le seuil, puisqu’il n’y a pas de vies en jeu, et que l’expérience met en jeu des techniques de manipulation génétique assez routinière, il n’y a pas lieu de choisir un seuil très élevé ou très bas. On opte donc pour le standard α = 0.05.
b.3. Chercher le test
Le test est de la forme :

pour lequel la valeur  ~ N(0,1). Après un examen dans une table N(0,1), on trouve que pour la valeur s(α / 2) = 1.96 (une valeur à retenir puisqu’elle va revenir très souvent), 5% de la distribution est située soit en bas de – 1.96 soit en haut de + 1.96 (car Pr( Z < 1.96) = 0.975 d’où Pr( Z > 1.96) = 0.025 et Pr( Z < -1.96) = 0.025.
~ N(0,1). Après un examen dans une table N(0,1), on trouve que pour la valeur s(α / 2) = 1.96 (une valeur à retenir puisqu’elle va revenir très souvent), 5% de la distribution est située soit en bas de – 1.96 soit en haut de + 1.96 (car Pr( Z < 1.96) = 0.975 d’où Pr( Z > 1.96) = 0.025 et Pr( Z < -1.96) = 0.025.
b.4. Appliquer le test et conclure
Le chercheur réalise sa recherche et trouve 230 personnes affectées sur 1000. Cette proportion est proche de 1⁄4. Est-ce différent? Nous calculons

Comme 1.46 n’est pas plus grand que notre valeur critique 1.96, nous ne rejetons pas l’hypothèse nulle.
Le chercheur conclu que les résultats obtenus sont –à nouveau- compatibles avec le modèle standard de transmission des gènes. Une prédiction faite par ce modèle n’a pas été rejetée par des résultats empiriques. Il est bien entendu qu’il existe peut-être d’autres modèles qui font cette même prédiction. Finalement, notons au passage qu’il est possible qu’un
modèle non standard prédise aussi une proportion de 1⁄4 pour le syndrome de Bezières. Donc, obtenir un quart de la population avec le syndrome de Bezières ne démontre rien. C’est pourquoi on appelle H0 l’hypothèse nulle. Si on ne rejette pas H0, nous conservons le statu quo quant à nos connaissances scientifiques. Si le chercheur avait rejeté H0 cependant, il aurait été l’instigateur d’une importante révolution scientifique.
4.2. Test sur deux proportions
Un aspect intéressant de l’utilisation de l’approximation normale est qu’il permet un nouveau test portant sur des proportions: Plutôt que de vérifier si une proportion observée dans un échantillon est compatible avec une prédiction à priori (p0), on peut aussi vouloir comparer deux échantillons pour voir s’ils exhibent la même proportion d’un certain trait. Ici, il n’y a pas de valeur prédite à priori, mais deux proportions observées dans deux échantillons X et Y.
a. idée générale du test
Comme précédemment, nous codons un « succès » avec 1 et un « échec » avec 0. Nous ne savons pas quelle est la proportion réelle p0, mais il s’agit par hypothèse de la même dans les deux cas, donc![]() – p0 vaut environ zéro, et de même pour
– p0 vaut environ zéro, et de même pour ![]() – p0. Si nous soustrayons les
– p0. Si nous soustrayons les
deux, on doit donc aussi obtenir environ zéro, mais (![]() – p0 ) – (
– p0 ) – ( ![]() – p0 ) =
– p0 ) = ![]() –
– ![]() .Autrement dit, la différence entre les deux proportions observées, si elles sont tirées d’une même population, doit égaler zéro car E(X – Y) = E(X) – E(Y) = 0 si X et Y sont tirés de la même population.
.Autrement dit, la différence entre les deux proportions observées, si elles sont tirées d’une même population, doit égaler zéro car E(X – Y) = E(X) – E(Y) = 0 si X et Y sont tirés de la même population.
Pour pouvoir normaliser la différence, par quelle variabilité doit-on diviser? Doit-on utiliser la variabilité du premier échantillon, la variabilité de second ou la variabilité des deux échantillons confondus? Le troisième choix est le bon. Ce que nous cherchons, c’est la variabilité de notre soustraction des deux proportions. Pour y arriver, deux points sont nécessaires: Premièrement, la variance Var(X – Y) = Var(X) + (-1)2Var(Y) (voir cours 2), soit Var(X) + Var(Y). Il s’agit d’un principe très général qui reviendra à toutes les fois que l’on compare la différence entre deux échantillons : Les variances de chaque échantillon s’additionnent.
Deuxièmement, nous avons vu au point (a) que la variance d’un échantillon X s’obtient par
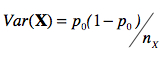
Dans la pratique (passe de mammouth no 1), le test est plus puissant si nous estimons la variabilité présente dans l’échantillon X en joignant les échantillons X et Y ensemble. Il en va de même pour estimer la variabilité présente dans Y. Puisque la variance d’un échantillon est égale à la variance de l’autre échantillon par hypothèse, la variance présente dans les deux échantillons devrait être la même. Soit ![]() la proportion totale de un autant dans X que dans Y.
la proportion totale de un autant dans X que dans Y.
![]() peut être calculé sur l’échantillon total, ou indirectement si vous connaissez
peut être calculé sur l’échantillon total, ou indirectement si vous connaissez ![]() et
et ![]() , en faisant une moyenne pondérée des deux (lorsque la taille des échantillons est inégale):
, en faisant une moyenne pondérée des deux (lorsque la taille des échantillons est inégale):

où nX donne la taille de l’échantillon X et nY la taille de l’échantillon Y.
En combinant les deux points ensemble, on obtient que la variance de notre différence de moyenne est la somme des deux variances (estimées de la même façon) divisée par la taille de leurs échantillons respectifs :

b. Structure du test
b.1. Postulats
Le test est basé sur les postulats que chaque essai est un essai de Bernoulli et que le nombre d’observations dans chacun des échantillons est élevé (n > 20). Chaque observation est codée en zéro ou en un.
b.2. Hypothèses et seuil
L’hypothèse nulle est que les deux échantillons sont issus de la même population et montre donc une même proportion p, cette valeur n’étant pas spécifiée. L’hypothèse alternative est que soit (unidirectionnel) (a) la proportion réelle dans la population d’où provient X est plus grande que la proportion dans la population d’où provient Y, (b) la proportion réelle dans la population d’où provient X est plus faible ou (bidirectionnel) (c) la proportion dans la population d’où provient X est différente, plus grande ou plus basse. Dans le cas c, le test est dit bicaudal. On note, selon le cas H0: pX =pY ,et (a) H1:pX >pY , (b) H1: pX < pY ou (c) H1: pX ≠ pY. Le choix de l’hypothèse alternative dépend du contexte théorique.
Pour continuer l’exemple du syndrome de Bezières, le chercheur fait remarquer que la proportion de 1⁄4 doit être universelle. Il procède donc à une expérience 3 en chine. Un échantillon Y est tiré et il observe une proportion de 420 personnes souffrant du syndrome sur 2000 (soit une proportion de 0.21). Pour savoir si la population chinoise est homogène avec la population canadienne quant à la présence du syndrome, il pose le test :
H0:pX =pY
H1: pX ≠ pY
On opte à nouveau pour le standard α = 0.05. b.3. Chercher le test
Le test est de la forme :

pour lequel la valeur  ~ N(0,1). Après un examen dans une table N(0,1), on trouve encore la valeur s(α / 2) = 1.96 (une valeur à retenir puisqu’elle va revenir très souvent) pour laquelle 2.5% de la distribution est située soit en bas de – 1.96 et 2.5% en haut de + 1.96.
~ N(0,1). Après un examen dans une table N(0,1), on trouve encore la valeur s(α / 2) = 1.96 (une valeur à retenir puisqu’elle va revenir très souvent) pour laquelle 2.5% de la distribution est située soit en bas de – 1.96 et 2.5% en haut de + 1.96.
b.4. Appliquer le test et conclure
Nous calculons premièrement la proportion de personnes souffrant du syndrome de Bezières dans les deux échantillons combinée en utilisant une moyenne pondérée:

Comme 1.25 n’est pas plus grand que notre valeur critique 1.96, nous ne rejetons pas l’hypothèse nulle. Le chercheur conclu que les deux échantillons ont la même incidence du syndrome de Bezières.
4.3. Test sur la médiane utilisant l’approximation normale et test sur observations couplées utilisant l’approximation normale
Le test de la médiane et le test sur observations couplées peuvent aussi être réalisés en utilisant l’approximation normale. Pour ce faire, il faut que n > 20. Comme dans les deux cas, la proportion testée est p0 =1/2, il s’ensuit que si n > 20, alors n × p0 > 10. La procédure est identique à celle décrite à la section 4.1.
Exercices
1. Pour décider si le nombre d’hommes se présentant à un bar populaire du centre-ville est supérieur à 50%, il faudrait utiliser un test basé sur la distribution :
a) Binomial unicaudal
b) Normal bicaudal
c) de proportion
d) Normal unicaudal
e) de Student t
2. Les paramètres d’une population son presque toujours estimés
a) Vrai
b) Faux
3.La variabilité de la population est sous- estimée par la dispersion de l’échantillon
a) Vrai
b) Faux
4. Quel est la valeur critère pour un test binomial où p=1⁄2 avec n= 20, unicaudal utilisant un seuil de :
a) 1%
b) 5%
c) 10%
5. Quel est la valeur critère pour un test binomial où p = 1⁄2 avec n = 20, bicaudal utilisant un seuil de :
a) 1%
b) 5%
c) 10%
6. Pour estimer la variance de la population à l’aide d’un échantillon de 1500 participants, il est préférable que la formule comporte
a) n
b) n–1
7. Un article mentionne un groupe de sujets dont l’écart type est 23 et l’erreur type de 2.3, mais l’auteur a oublié de rapporté le nombre de sujets. Combien y en a-t-il?
8. Étant donné l’échantillon suivant ![]() = 21.08, n−1
= 21.08, n−1 ![]() = 3.66, NX = 13, calculez l’erreur type :
= 3.66, NX = 13, calculez l’erreur type :
9. Soit 10 sujets mesurés sous deux conditions : X = {15, 23, 30, 7, 3, 22, 12, 30, 5, 14} puis Y = {28, 19, 34, 19, 6, 26, 13, 47, 16, 9}. Est-ce que les sujets sont- meilleurs en Y?.
10. Est-ce que la médiane de cet échantillon est bien de 20? X = {1, 3, 5, 9, 10, 14, 15, 17, 21, 45, 49, 110, 230, 666, 7542}.
11. Un professeur met au point une nouvelle méthode didactique. Pour la tester, le professeur choisit un seuil
a) de 0.05 parce que c’est le seuil habituel
b) permettant de concilier les deux risques d’erreur (α et β).
c) très sévère parce que les conséquences d’une erreur α seraient catastrophiques
d) trèspeusévèrecarlesconséquences d’une erreur β seraient catastrophiques
Si vous remarquez des informations erronées ou manquantes, merci de le partager par les Commentaires.



