C2: Statistiques descriptives

Section 1 : Savoir n’est pas comprendre

Les distributions de fréquences et leurs représentations graphiques que nous avons vues au cours précédent donnent un aperçu de la répartition d’un ensemble de données. De plus, elles offrent aux chercheurs une façon empirique de vérifier la validité de leurs données. Cependant, ce n’est qu’un premier pas. Il faut ensuite obtenir des prises sur ces données brutes, des valeurs facilement communicables pour qu’un lecteur éventuel puisse se faire une idée des données sans devoir les énumérer. Ceci est le rôle de la statistique descriptive.

Pour comprendre l’importance de ces prises, imaginons un être surnaturel qui pourrait connaître pour n’importe quel moment dans le passé la position de la planète Mars. Il n’est pas clair que cette entité pourra dire où sera Mars dans un mois. En effet, pour extrapoler, il faut savoir comment généraliser nos connaissances antérieures (pour obtenir par exemple la loi du mouvement de Newton), puis évaluer des paramètres (le poids de Mars, du soleil). Ainsi, une connaissance parfaite d’un phénomène n’implique pas une compréhension des processus à l’oeuvre.

De la même façon, si cet être connaît toutes les positions et les vitesses des atomes d’eau contenus dans un verre, est-ce que cela implique qu’il connaisse sa température? Encore une fois, non. La température d’un liquide reflète la vitesse de déplacement moyenne des atomes le composant. Or, connaître la vitesse d’un atome particulier n’informe en rien sur la vitesse moyenne. Il faut compiler ces vitesses individuelles de façon à en extraire une information plus significative (la température).

En psychologie, si nous mesurons chez mille individus le temps nécessaire pour identifier un visage, nous allons obtenir mille mesures différentes. Que peut-on conclure? Que nous avons tous des processus différents pour reconnaître les visages? Nous sommes loin de l’idée d’une loi. Il faut plutôt chercher à identifier ce qui est commun à l’ensemble des participants. L’utilisation de statistiques descriptives permet d’atteindre ce but.

Section 2 : Statistiques de la tendance centrale

Les statistiques de la tendance centrale (ou encore les mesures de la tendance centrale) ont pour objectif de donner une idée de la localisation des données brutes (i. e. la localisation de leur distribution). Les données sont-elles généralement grandes? Petites? Plusieurs mesures de la tendance centrale existent, dont la plus fréquente est la moyenne arithmétique (souvent appelée tout simplement la moyenne). Dans tous les cas, une mesure de la tendance centrale indique si la distribution est située plus à droite ou plus à gauche de l’échelle.

Dans l’exemple de la Figure 1, la taille (en cm) de deux échantillons (fictifs) a été obtenu chez 400 individus de sexe féminin et masculin respectivement. On voit en regardant les distributions que la distribution des tailles chez les femmes est légèrement décalée vers la gauche par rapport à celle des hommes. Toutes les mesures de tendance centrale devraient refléter ce point.

Lorsque l’on calcule le Mode (), la Médiane (), la Moyenne arithmétique (), la Moyenne géométrique () et la Moyenne harmonique (), on obtient les résultats suivants:

Comme on le voit, les cinq mesures de la tendance centrale indiquent bien que la distribution des femmes est légèrement plus à gauche que celle des hommes.

La médiane et le mode sont des statistiques qui sont surtout utiles quand la distribution contient des valeurs extrêmes puisque ces mesures sont peu influencées par des scores marginaux. En économie par exemple, le revenu médian est beaucoup plus utilisé que le revenu moyen, considérant qu’il existe une poignée de personnes qui ont des revenus dépassant les milliards de dollars (scores extrêmes).

Note sur la nomenclature

Vu le nombre important de symboles que nous allons manipuler, il est important d’avoir une nomenclature uniforme.

Dans tout ce qui suit, nous utilisons une lettre de la fin de l’alphabet en majuscule pour dénoter des échantillons, telles X, Y, Z. Lorsqu’une statistique est calculée sur un échantillon, nous ajoutons un symbole sur la lettre dénotant l’échantillon.

Des exemples de statistiques calculées sur l’échantillon X sont ,, , etc. Contrairement à X qui représente un ensemble de plusieurs valeurs, représente une valeur unique pour un échantillon donné.

Dans le cas de l’écart type (voir cours suivant), nous utilisons . Or, il existe deux façons de calculer l’écart type. Pour les distinguer, nous ajoutons à la gauche du symbole une étiquette, soit n ou n – 1: n , n−1 . L’étiquette ne représente pas une opération mathématique, seulement une indication:

Dans le passé, et sur beaucoup de calculatrices, ces symboles sont utilisés:

Leur principal défaut est de ne pas dire s’il s’agit de l’écart type pour l’échantillon X ou Y; cette ambiguïté n’existe pas avec n vs. n .

Une alternative à la médiane et au mode sont les moyennes. Il existe trois façons de moyenner les observations d’un échantillon, la moyenne géométrique, la moyenne harmonique, et la moyenne arithmétique. En règle générale, on observe que < < . Les moyennes utilisent toujours toutes les données brutes. Ainsi, chacune exerce une influence sur la moyenne obtenue (d’où l’importance de vérifier la validité des données extrêmes).

Les moyennes géométriques et harmoniques sont utilisées dans des situations particulières (et virtuellement jamais en psychologie). Par exemple, les économistes qui n’aiment pas utiliser la médiane vont utiliser la moyenne géométrique qui ressemble un peu à la moyenne (arithmétique) mais est un peu moins affectée par les données extrêmes (telles les milliardaires).

La moyenne arithmétique (appelée moyenne dans la suite) possède des propriétés mathématiques intéressantes (que nous expliquerons en détails dans l’encadré (7) au cours 5) : il s’agit d’une statistique efficace et sans biais. Pour ces raisons, la très grande majorité des tests statistiques sur la tendance centrale sont en fait des tests sur la moyenne.

La moyenne se calcule suivant cette formule simple sur les données brutes, 1/n sum{i}{}{X_i}. Cette expression peut se réorganiser comme suit : sum{i}{}{1/n X_i} où le 1/n indique tout simplement que cette donnée est présente 1 fois sur n. Si certaines données brutes Xi se répetent, il est possible de gagner du temps en utilisant plutôt : sum{i}{}{f X_i} où f est la fréquence relative de la donnée brute (i. e. la proportion de fois qu’elle a été observée).

Comment faire un graphe

Quand vient le temps de présenter vos résultats, une façon très efficace consiste à présenter des graphes de vos statistiques descriptives (en règle générale, la moyenne, quoique l’écart type est aussi présenté à l’occasion. Pour faire des graphes qui soient clairs, il y a certains points qu’il ne faut pas oublier :

Tous les graphiques doivent avoir un titre (contrairement à ceux trouvés dans ces notes de cours) qui commencent en général par « Figure x : … ».

Les axes doivent avoir une indication de la variable illustrée ainsi que, le cas échéant, de son unité de mesure entre parenthèses (par exemple, temps (ms)). De plus, le système métrique doit être utilisé dans tous les cas.

Les points doivent utiliser la majorité de l’espace sur le graphe.

Si l’abscisse est un échelle de type I, utiliser de préférence un graphe en histogramme; si l’échelle est de type II, utiliser de préférence une courbe.

Voici à la Figure 2 quelques exemples de graphes présentant des statistiques pour des études où il n’y a qu’une seule V. I.

Quand l’étude manipule deux V. I., utilisez des histogrammes regroupés (clustered) ou encore plusieurs lignes, comme à la Figure 3. Dans ce cas, il ne faut pas oublier de mettre une légende (note : ces graphiques montrent l’erreur type, voir l’encadré suivant).

À l’occasion, des données avec deux V. I. peuvent aussi se prêter à un graphique en trois dimensions, comme c’est le cas dans la Figure 4.

Finalement, dans le cas où plus de 2 V. I. sont utilisées, il faut utiliser des panneaux distincts pour chaque graphique, avec une étiquette précisant le niveau d’une des V. I. sur chacun. Dans ce dernier cas, une seule légende pour l’ensemble des panneaux peut être utilisée comme c’est le cas à la Figure 5.

Section 3 : Statistiques de la variabilité

Les mesures de tendances centrales vues précédemment sont informatives, mais insuffisantes pour décrire une distribution. Il est aussi utile de connaître la dispersion des données.

Il existe plusieurs façons de calculer la dispersion des données brutes. Par exemple, on pourrait calculer la distance entre les deux extrêmes (l’étendue, que nous avons vu dans le cours 1). Cependant, seulement deux données sont utilisées (Min(X) et Max(X)), rendant cette mesure très sensible aux erreurs d’échantillonnage (données extrêmes). Une autre façon de mesurer la variabilité serait de calculer la moyenne des distances entre toutes les paires de scores. Cependant, nous serions confrontés à un nombre astronomique de paires de scores possibles (pour n données, il existe n (n – 1) /2 paires, un nombre qui devient rapidement énorme; essayez avec n = 100).

La méthode la plus usitée prend comme point de départ que la moyenne se situe au centre de la distribution. On peut donc l’utiliser comme point de référence. Imaginons que l’on calcule la distance entre chaque point Xi et la moyenne des points . Si on fait la somme de toutes ces distances et divisons par n, noté 1/n sum{i}{}{} (Xi-) nous n’aurons malheureusement pas une valeur de dispersion. En effet, la somme des distances entre chaque donnée brute et sa moyenne est toujours nulle. En effet, en terme mathématique :

C2.9

Autrement dit, à cause de la position centrale de la moyenne, les distances négatives des données plus petites que la moyenne sont exactement contrebalancées par les distances positives des données plus grandes. Pour vous en convaincre, faites le test avec ces données : X = {1, 2, 3, 4, 5, 6, 7}.

(Si on ignore la multiplication par 1/n, ce résultat stipule que la somme des écarts à la moyenne donne toujours zéro. C’est un résultat qui va revenir souvent par la suite pour simplifier des formules plus complexes).

Pour contourner le problème, nous élevons chaque distance au carré, obtenant ainsi une série de carrés ayant tous des valeurs positives. Le résultat est appelé la variance, dont la formule est

1/n sum{i}{}{} (Xi-)²

Comme nous allons le voir dans l’encadré (8) du cours 5, la variance d’un échantillon est biaisée. En effet, même si l’échantillon reflète dans une certaine mesure la variabilité de la population dont il est tiré, il est probable que parmi ce petit nombre de données brutes (par rapport à la taille de la population entière), les données les plus extrêmes soient sous représentées (simplement parce qu’il y en a peu dans la population). En conséquence, la variabilité de la population sera sous-estimée par la variabilité de l’échantillon.

Pour éviter ce biais, il faut augmenter la valeur de cette estimation. Cependant, cette correction doit s’atténuer lorsque la taille de l’échantillon est très grand. Cette correction est donc fonction de n. On démontrera à l’encadré (8) du cours 5 que la correction adéquate est de multiplier la variance de l’échantillon par n/(n-1) de façon à obtenir une variance qui reflète le fait que notre échantillon soit forcément affecté par une espèce de régression vers la moyenne. Si n est petit, la correction est appréciable et la variance estimée de la population est plus grande. Si n est très grand, la correction devient négligeable. Dans la suite, l’on va distinguer la variance corrigée pour le biais d’un échantillon, notée n-1² de la variance biaisée d’un échantillon, notée n² .

Prenez le temps de vérifier que votre calculatrice de poche peut calculer la variance d’un échantillon corrigée pour le biais (parfois, le bouton est noté S_n-1² ou encore σ_n-1²). C’est la seule mesure d’intérêt.

La variance étant une mesure au carré, on rapporte souvent la racine carrée de la variance, que l’on appelle l’écart type non-biaisé (ou corrigé pour le biais) d’un échantillon, et noté _n-1.

Une façon simple de bien comprendre ce qu’est la variabilité mesurée par l’écart type _n est de se poser la question suivante : Supposons que je prends une mesure de mon échantillon au hasard, à quelle distance de la moyenne se trouvera-t-il approximativement?

On a déjà vu que dans l’ensemble, la déviation à la moyenne s’annule; il faut une approche qui ne tienne pas compte du signe de la déviation. On va donc considérer le carré (car élever au carré enlève le signe) puis prendre la racine carrée. En moyenne, la distance entre une donnée quelconque et sa moyenne est donnée par :

C2.10

Autrement dit, en prenant une donnée au hasard, elle a toutes les chances d’être à ± un écart type de la moyenne de l’échantillon. À partir d’une donnée unique, l’erreur que vous faites pour estimer la moyenne est de plus ou moins un écart type, en moyenne.

L’erreur type

Une estimation basée sur un échantillon restreint de données brutes qui exclut donc la majorité des valeurs de la population contient une certaine marge d’erreur. Cette erreur, nous l’appelons l’erreur type. Il existe deux sources d’imprécision pour estimer l’erreur type.

a) Imaginons que nous choisissons aléatoirement deux échantillons de même taille à l’intérieur d’une même population. Nous obtiendrons assurément deux moyennes légèrement différentes tout simplement parce que nos échantillons ne sont pas identiques. Or, la dispersion de ces moyennes dépend de la taille des échantillons sélectionnés. Des échantillons extrêmement petits ont une plus grande variabilité et sont donc imprécis pour estimer la moyenne de la population. D’un autre côté, si on choisit deux échantillons très grands, les moyennes qui en résultent varieront très peu. Pour exprimer ceci, on dira que l’erreur d’estimation est inversement proportionnelle à n (c’est à dire proportionnel à 1 / n).

b) Le deuxième déterminant de la précision d’un estimé est la variabilité qui existe à l’intérieur même de la population. Si la population ne contient que des mesures constantes, les échantillons seront composés de cette même constante, et la variance sera zéro, ce qui signifie pas d’erreur dans l’estimé. Par contre, si la variabilité est très grande dans la population, nos deux échantillons seront aussi sans aucun doute très différents. De fait, les échantillons reflètent plus ou moins bien la dispersion de la population. Ainsi, l’erreur type sera proportionnelle à la variance de la population (inconnue mais que l’on peut estimer par la variance non biaisée _n-1²

La précision du calcul d’une moyenne, que l’on nomme l’erreur type (ou en anglais Standard error parfois traduit par erreur standard), notée SE, dépend donc de ces deux facteurs, que l’on peut tout simplement multiplier. Pour avoir une erreur qui soit dans la même unité que la moyenne, on extrait la racine carrée. On obtient donc :

Il est à noter que la formule d’erreur type varie selon le type de statistique dont l’on veut une marge d’erreur. Par exemple :

Il est commode (quoique rarement fait) de rapporter dans un texte la moyenne plus ou moins l’erreur type (par exemple, la longueur est de 224 mm ± 14 mm). Comme on le verra dans le cours 4, l’erreur type est en fait très proche de la méthode du test t. De plus, il est très fortement recommandé de mettre dans tout graphique représentant des moyennes une barre d’erreur dont la hauteur est donnée par l’erreur type. Des logiciels comme SPSS peuvent calculer automatiquement cette barre d’erreur sur demande.

Section 4. Relations fondamentales sur les moments statistiques

Il existe quelques formules clefs qui vous donnent la moyenne ou la variance quand vous transformez les valeurs de votre échantillon à l’aide d’une constante multiplicative a et d’une constante additive b. Dans la suite, je dénote la moyenne par E(X), et la variance _n-1² par Var(X).

E(aX+b) = aE(X)+b

Var(aX+b) =a²Var(X)

Var(X) = E(X²)-E² (X)

Autrement dit, si vous additionnez une constante b à chacune de vos données brutes, la moyenne s’en trouve affectée, mais pas la variance (car b n’amène aucune variabilité). N’oublions pas cette relation que nous avons déjà prouvée au cours précédent:

E(X-)=0

Finalement, si vous manipulez deux échantillons indépendants, il existe ces trois relations :

E(X + Y) = E(X) + E(Y)

E(X ×Y) = E(X) × E(Y)

Var(X + Y) = Var(X) + Var(Y)

Ces relations seront souvent utilisées dans les preuves mathématiques.

Section 5. Autres moments statistiques et leur représentation visuelle

Pour bien décrire une distribution de données brutes, il est indispensable de rapporter la moyenne et l’écart type. En règle générale, ces deux statistiques sont les plus signifiantes, et les plus à même d’être retrouvées dans un article scientifique. Si on illustre une distribution quelconque (ses fréquences obtenues ou encore sa fonction de masse PDF, si connue) en utilisant un graphique avec une courbe continue, on peut localiser visuellement la moyenne en trouvant le point où la distribution serait en équilibre. Dans les deux exemples de la Figure 6, la moyenne se trouve à 170.

C2.13

On peut obtenir une appréciation visuelle de l’écart type en regardant la largeur de la distribution. Dans les exemples précédents, il est très clair que les données du graphe de droite présentent une plus grande variabilité que celles de gauche. Il est cependant plus difficile de voir que l’écart type est 20 dans le premier cas et de 15 dans le second. Dans ces exemples, les données étaient réparties symétriquement, ce qui fait que la moyenne coïncide avec la médiane et le mode. De plus, le centre de gravité se trouve au centre. Par contre, les distributions ne sont pas toujours symétriques, comme dans les deux exemples de la Figure 7.

C2.14

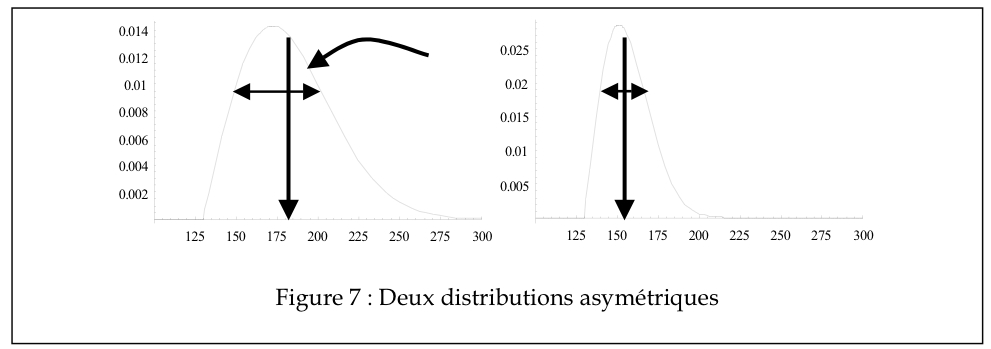
Encore une fois, la moyenne est le centre de gravité, légèrement à droite du mode puisque la partie droite s’étend beaucoup plus que l’autre. L’écart type se mesure aussi assez bien visuellement, étant de 13,9 et 6.9 respectivement. Cependant, il devient clair que l’asymétrie de ces distributions est un aspect important des données et qu’il faudrait rapporter une statistique mesurant cet état de fait. L’exemple de la Figure 8 donne un exemple où l’asymétrie est encore plus extrême. Lorsqu’une distribution n’est pas symétrique, le mode, la moyenne et la médiane diffèrent.

C2.15

Pour quantifier l’asymétrie (Skewness en anglais), on utilise la formule suivante :

Le résultat nous indique la direction de l’asymétrie. Il existe trois cas possibles : Si > 0, l’asymétrie est positive et la distribution s’étale plus vers les valeurs élevées de la variable. On dit qu’elle a une longue queue à droite. Si = 0, la distribution est parfaitement symétrique. Si < 0, l’asymétrie est négative, et la queue est plus longue à gauche. [Notez que SPSS multiplie par n²/((n-1)(n-2)) le résultat ci-haut; la valeur retournée par le logiciel est donc légèrement différente, mais le signe positif ou négatif reste le même.]

Finalement, il peut arriver que l’aplatissement de la distribution soit inusité. Une statistique qui donne un indice de cet aplatissement est la kurtose (Kurtosis). Elle se calcule avec la formule :

Une kurtose de 3 indique une rondeur typique de la distribution en pointillé (qu’on appelle mésocurtique). Si est inférieur à 3, ceci indique une distribution plus pointue et plus haute (qu’on appelle platycurtique). Dans le cas contraire (Qu’on appelle leptokurtique), les queues de la distribution s’étendent plus loin que pour la distribution normale, à écart type équivalent. Comme la valeur 3 est une indication de kurtose neutre, certains auteurs (et SPSS) recommandent de soustraire 3 à la formule ci-haut. Dans la figure 9, les trois distributions ont une moyenne de 0, un écart type de 1, et sont symétriques (skewness = 0) mais varient selon la kurtose.

C2.18

Les statistiques présentées jusqu’à présent sont aussi appelées des mesures de la position (moyenne), de l’échelle (écart type), de l’asymétrie (Skewness) et de l’aplatissement. De plus, l’échelle, l’asymétrie et la kurtose sont aussi appelées des moments μ de degré r (2, 3, et 4) respectivement pour la raison que dans leurs calculs, on utilise la somme des écarts à la moyenne élevée à la puissance r : C2.19

Comme on l’a dit précédemment, la somme des écarts à la moyenne (sans exposant) donne zéro. On a donc que μ₁ = 0. De plus, on a ces relations

Il existe d’autres moments de niveau supérieur (une infinité en fait), mais ceux-ci deviennent de plus en plus abstraits, et imperceptibles quand on inspecte visuellement une distribution.

Section 6. Quantiles

Il peut arriver lorsque la distribution des données est particulière ou encore quand les hypothèses des chercheurs portent sur celle-ci que rapporter seulement les trois premières statistiques ne soit pas suffisant. Dans ce cas, une image vaut mille mots : rapportez le graphe de la distribution des fréquences observées. Une alternative quelquefois utilisée, qui remonte au début du siècle quand les méthodes pour réaliser des graphes étaient moins facilement accessibles, est de rapporter les quantiles (parfois appelés les N-tiles). L’idée est de rapporter quelques points le long de la distribution cumulative des fréquences. Avec ces quelques points, le lecteur peut extrapoler pour obtenir la distribution complète. Le nombre de points à rapporter est variable, mais souvent, on utilise les quartiles (N = 4 points), les déciles (N = 10 points) et les centiles (N = 100 points). Bien entendu, le nombre de points rapportés N doit être nettement inférieur au nombre d’observations n, pour que les valeurs des quantiles soient stables.

C2.22

Si vous rapportez les quartiles (N = 4), vous devez rapporter les points tels que 25%, 50%, et 75% des données observées y soient inférieures. Ces points sont les frontières entre le premier quart des données et le second, entre le second et le troisième, et entre le troisième et le dernier quart des données. De façon, générale, pour un N choisi, vous rapportez N – 1 valeurs situant les fréquences relatives 1/N, 2/N, … (N-1)/N. Les quantiles s’obtiennent aisément du graphique des fréquences cumulatives (que vous intrapolez en reliant ensemble les centres de classes). Dans l’exemple sur la gauche, où l’on voit les fréquences cumulatives relatives (i.e. entre 0 et 1) de la taille des hommes vues au cours précédent, localisez les points sur l’abscisse tels que l’ordonnée soit 25%, 50% et 75%. Notez en passant que le point où la fréquence relative est de 50% est par définition la médiane. Dans notre exemple, on trouve les valeurs {157, 172, 185}. Plusieurs logiciels peuvent faire ce travail d’intrapolation efficacement.