C12: Corrélation et régression
Section 1. À Washington, ce sont les cigognes qui apportent les bébés
L’étude des corrélations entre deux variables est un domaine qui peut parfois révéler beaucoup sur les mécanismes sous-jacents. Par exemple, chez les conducteurs automobiles, il existe une très forte corrélation entre le fait de posséder un téléphone cellulaire et le nombre d’accident automobile. Évidemment, la cause de cette corrélation est très simple: les conducteurs qui parlent dans leur cellulaire sont beaucoup moins attentifs à la route et ont donc des réactions plus lentes en cas de danger, ce qui augmente la probabilité d’accidents. On peut presque dire que la possession d’un cellulaire cause un accroissement des accidents. Cependant, toutes les corrélations ne sont pas aussi faciles à comprendre. À Washington, un journaliste a découvert qu’il existe une très forte corrélation entre le fait d’avoir un nid de cigogne sur sa demeure et le fait d’avoir des enfants. D’où la conclusion (erronée) que les cigognes apportent les bébés.
En fait, pour comprendre cette corrélation, il faut faire intervenir un grand nombre de facteurs indirects (qui n’ont pas été inclus dans la recherche du journaliste) qui ont aussi un effet sur le fait d’avoir des enfants: Pour avoir un nid de cigogne, il faut une cheminée et donc, une maison. Les maisons sont très dispendieuses dans cette région des États-Unis. Les couples aisés sont plus à même d’avoir des enfants aux États-Unis que les couples plus pauvres. Tout ces facteurs mis ensemble montre que le fait d’avoir un nid de cigogne ne démontre seulement que le couple est plus aisé, et donc, plus à même d’avoir des enfants. La présence d’une cigogne est un signe très indirect, et certainement pas la cause, du nombre d’enfants.
Section 2. Statistique de corrélation
Qu’entend-t-on par corrélation? Supposons deux échantillons sur un groupe, par exemple, quotient intellectuel et habilité en lecture. On s’attend à ce que ces deux mesures varient ensembles. C’est à dire que si une personne a un score élevé sur une mesure, l’autre mesure devrait aussi être élevée. Inversement, si une personne a un score faible sur une mesure, l’autre devrait aussi être faible. Dans ce cas, les mesures sont dites positivement corrélée.
Imaginons par opposition, deux autres mesures, l’habilité en lecture et le temps pour lire un passage donné. Dans ce cas-ci, on s’attend plutôt à ce qu’une personne avec un score élevé dans l’habileté en lecture montre un score petit (rapide) en lecture, et vice-versa. Dans ce second cas, les mesures sont dites négativement corrélée.
La corrélation est une statistique qui caractérise l’existence ou l’absence d’une relation entre deux échantillons de valeurs prise sur un même groupe de sujets. Le coefficient de corrélation permet de quantifier cette relation 1- par le signe de la corrélation (positive et négative), et par la force de cette corrélation. Le degré de corrélation, comme nous le verrons plus loin, se mesure sur une échelle de 0 à 1. Zéro signifie une totale absence de corrélation entre les deux mesures, alors que 1 signifie une corrélation parfaite, c’est à dire que connaître la valeur d’une mesure nous permet de connaître exactement la valeur de l’autre. Les illustrations de la Figure 1 (appelées « scatterplot » quand on illustre une mesure en fonction d’une autre mesure) donnent quelques valeurs possibles pour le coefficient de corrélation.
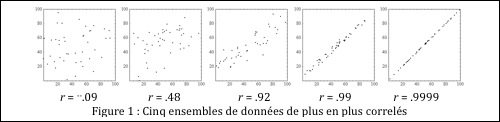
On peut concevoir le coefficient de corrélation comme un indice de la qualité de la droite idéale passant par les points (ou encore comme la pente quand les valeurs des deux variables ont étés normalisée -transformée en cote z). Les moyennes des deux variables sont alors zéro. et la variance est 1. Les données autant de X que de Y s’étendent vraisemblablement entre –3 et +3.
On se rend compte que dans le cas où r = 0, les valeurs Y élevées pourraient être autant associées à des valeurs X élevées qu’à des valeurs X basses. Et vice-versa. La meilleure prédiction possible de Y ne dépend pas de la connaissance de X. La connaissance de X ne donne aucune information sur Y.
Comme on le voit, le nuage de point devient de plus en plus étroit au fur et à mesure que le coefficient devient élevé. Quand r est à son maximum (1), les données transformées de X sont parfaitement prédites par les données transformées de Y, c’est à dire
. Dans le cas où r = -1, la relation est toujours vraie, sauf pour un signe moins : .
Il faut cependant faire attention de ne pas confondre corrélation et causation. Le fait que l’habilité en lecture soit fortement corrélée avec le quotient intellectuel ne signifie pas que l’habilité en lecture détermine le Q. I. de l’individu. Et vice-versa.
Il arrive aussi parfois que ce ne soit pas deux V. D. qui soient mises en corrélation, mais plutôt une V.D. avec une variable indépendante, telle la condition dans laquelle se trouve le sujet. Dans ce dernier cas, la V.I. est toujours mise sur l’axe des abscisses.
Section 3. Corrélation simple
Nous noterons rXY le coefficient de corrélation entre deux échantillons X et Y. Il est aussi souvent appelé le coefficient de corrélation de Pearson, du nom de son inventeur, pour le distinguer d’autres indices de corrélations (tel le coefficient de Spearman).
3.1. Calcule du r
Pour calculer le coefficient de corrélation, il faut premièrement pouvoir calculer la covariance entre deux échantillons. On se rappelle que la variance (non biaisée) se calcule comme suit :
La covariance est une mesure de la variance présente dans deux échantillons simultanément. L’idée étant que si les deux échantillons covarient, la covariance devrait être grande, alors que s’ils ne covarient pas, la covariance devrait être modérément faible. Une façon d’atteindre cette mesure est d’utiliser le produit des différences, comme suit :
Dans cette équation, si Xi tend à être très supérieur à sa moyenne en même temps que Yi, la somme sera grande, indiquant une forte covariation.
La mesure de covariation est exprimée en unité de X fois l’unité de Y. Dans le premier exemple ci-haut, la covariation serait exprimé en point de Q.I par mots lus. Pour éliminer ces unités, on peut diviser par les écarts types des échantillons pris individuellement. Cette division a aussi pour résultat de normaliser la covariance entre –1 et 1, ce qui est donc l’indice de corrélation souhaité:
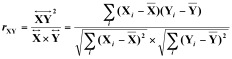
Ce que nous avons en fait, c’est un ratio entre combien de variation les deux mesures ont en commun divisée par la quantité de variation qu’elles pourraient avoir au plus. Si on élève r au carré, r2 donne la quantité de variance en commun entre les deux échantillons. On parle aussi souvent de « pourcentage de la variance expliquée », car si on prend le point de vue que, disons, X explique les résultats obtenus en Y, une certaine quantité de variance en X explique la variance en Y, et cette quantité est donnée par r2. Autrement dit, si nous connaissons la variable X, l’incertitude à propos de la variable Y est réduite de moitié.
Une autre façon d’illustrer la variance expliquée est sous la forme d’un diagramme de Venne. Dans ce cas, on peut voir r2 en terme de superposition de cercles.
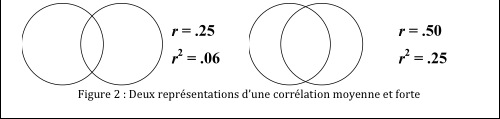
Exemple.
Soit une recherche où un chercheur désire examiner la relation qu’il peut exister entre l’habilité en lecture (X) et le nombre d’heures de lecture par semaine (Y). X est mesuré en laboratoire à l’aide d’un test d’habilité en lecture alors que Y est estimé par les sujets eux-mêmes. 10 sujets ont été échantillonnés. Les résultats sont :
|
sujets |
Xi |
Yi |
||
|
1 |
20 |
5 |
||
|
2 |
5 |
1 |
||
|
3 |
5 |
2 |
||
|
4 |
40 |
7 |
||
|
5 |
30 |
8 |
||
|
6 |
35 |
9 |
||
|
7 |
5 |
3 |
||
|
8 |
5 |
2 |
||
|
9 |
15 |
5 |
||
|
10 |
40 |
8 |
||
|
Moyenne Écart type |
20.0 15.09 |
5.0 2.91 |
||
Pour calculer la covariance à l’aide d’une calculatrice, il n’existe malheureusement pas de touche « covariance ». Il faut donc préparer les données en calculant manuellement les termes 
. Ce que l’on fait dans le tableau suivant :
Dans la dernière colonne, nous ne calculons pas l’écart type car il s’agit déjà de déviations à la moyenne. Il faut en faire la somme puis diviser par (n – 1) pour obtenir la covariance. Nous obtenons donc 
. C’est à dire une corrélation positive très proche de 1. Est-elle significative?
3.2. Test sur le coefficient de corrélation de Pearson
Lorsqu’on veut tester si un coefficient est significatif, on pose en fait l’hypothèse nulle que le coefficient est zéro. Il existe une démonstration qui indique que le coefficient se distribue normalement autour de zéro si la variance est stable pour un Xi donné. La variabilité du coefficient autour de zéro est inconnue. Cependant, la variance qui reste à expliquer (1 ‑ r2) est un bon estimateur de la variance du coefficient. Ces indicateurs nous permettent de construire un test, semblable au test t (normalité du numérateur, et variance estimée au dénominateur).
a.1 Postulats
Les scores individuelles se distribuent normalement et la variance entre les scores, quand Xi s’accroît reste constante.
a.2: Hypothèse et seuil
Les hypothèses sont de la forme :
H0 : rXY = 0
H1 : rXY ≠ 0
Il s’agit d’un test bidirectionnel. Dans ce cas, il faut utiliser un test bidirectionnel et donc répartir a en deux. Un test unicaudal est aussi possible si les hypothèses de recherches prédisent un signe précis au coefficient de corrélation. Dans ce cas, le test qui suit ne doit pas utiliser la valeur absolue. Le seuil a est libre (souvent 5%).
a.3. Chercher le test
Le test est de la forme :
rejet de H0 si 
> s(a/2)
dans lequel la valeur se distribue comme un t avec (n – 2) degrés de liberté. Ici, n est le nombre d’observations dans les échantillons X et Y. On soustrait par deux car le calcul du coefficient rXY nécessite le calcul de deux moyennes. Pour notre exemple précédent, un regard dans la table t nous donne comme valeur critique s (5%/2) avec 8 degrés de liberté : 2.306.
a.4. Appliquer le test et conclure
Nous calculons 
. La valeur obtenue est bien plus grande que la valeur critique. Nous pouvons rejeter H0 et conclure qu’il existe bel et bien une corrélation significative entre l’habilité en lecture et le nombre d’heures de lecture par semaine rapporté par les sujets, et que cette corrélation est positive (t(8) = 7.60, p < .05).
3.3. La droite de régression
Soit la situation où nous observons bel et bien une corrélation significative entre une variable Y et une variable X. L’étape suivante est de quantifier la relation. Par exemple, pour chaque changement d’une unité en X, de combien change la valeur attendue en Y?
Une façon d’y parvenir est de réaliser un scatterplot des données, puis de trouver la droite idéale qui traverse le mieux les données. La droite la plus proche de tous les points est appelée la droite de regression. Comme toujours, l’équation d’une droite est donnée par :
dans laquelle est la pente de la droite, et a, l’ordonné à l’origine (l’endroit où la droite coupe l’axe des Y). Il existe une méthode simple pour calculer ces paramètres de la droite de régression. En effet, la pente (le degré d’élévation de Y en fonction de X) est donnée comme le rapport de la covariance sur la variance des X. Donc :
Si le rXY est déjà disponible, on peut gagner du temps avec la formule équivalente :
Pour trouver l’ordonnée à l’origine, on note qu’en utilisant les moyennes comme un couple de valeurs possibles, on obtient :
ou encore
Dans notre exemple précédent, on trouve que 
et que
. Donc, on trouve que pour chaque point d’accroissement dans les X, les Y s’accroissent de près de 0.2 unité. De plus, si X est zéro, on s’attend à ce que Y soit de près de 1.4. Faîtes le graphique des données et de la droite de régression, et vérifiez que les valeurs sont appropriées.
3.4. Test sur la pente de la régression
Il va de soi que si la régression est significative, ceci indique que la pente b diffère de zéro. Cependant, il existe certaines situations où on voudrait savoir si la valeur obtenue pour b est égale à une certaine valeur définie à priori par une théorie.
a.1 Postulats
Avec les mêmes postulats que pour le coefficient de corrélation, on peut construire une valeur impliquant la différence entre la pente obtenue et la pente attendue par la théorie qui soit distribuée comme une statistique t. L’utilisation de la table t vient du fait que la vraie variance des valeurs possibles de la pente n’est pas connue, mais estimée à partir des données.
a.2. Hypothèse et seuil
Les hypothèses sont de la forme :
H0 : bXY = b0
H1 : bXY ¹ b0
où b0 est une valeur fournie à priori par une théorie. Un test unicaudal est aussi possible si les hypothèses de recherches prédisent un signe précis au coefficient de corrélation. Dans ce cas, le test qui suit ne doit pas utiliser la valeur absolue. Le seuil a est libre (souvent 5%). Supposons dans notre exemple que l’on veuille savoir si la pente peut être de ¼ exactement.
a.3. Chercher le test
Le test est de la forme :
rejet de H0 si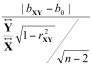
> s(a)
dans lequel la valeur 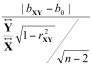se distribue comme un t avec (n – 2) degrés de liberté. Ici, n est le nombre d’observations dans les échantillons X et Y. On soustrait par deux car le calcul du coefficient rXY nécessite le calcul de deux moyennes. Pour notre exemple précédent, un regard dans la table t nous donne comme valeur critique s(5%) avec 8 degrés de liberté : 2.306.
a.4 Appliquer le test et conclure
Nous calculons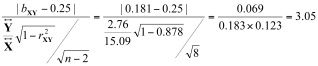 
. La valeur obtenue est bien plus grande que la valeur critique. Nous pouvons rejeter H0 et conclure que la pente est significativement inférieure à ¼ (t(8)=3.05, p < .05). Ceci permet de rejeter la théorie qui prédit une pente de ¼.
Section 4. Corrélations multiples
Jusqu’à présent, nous n’avons considéré que des corrélations entre deux variables. Il existe aussi des cas où trois variables ou plus sont impliquées. Par exemple, pour prédire le revenu familial d’un individu (Z), les indicateurs Degré de scolarité (X) et Revenu des parents (Y), pris individuellement n’expliquent peut-être qu’une partie de la variance, alors que lorsque les deux sont pris en considération simultanément, une bien meilleure prédiction peut être atteinte. Voir la Figure 3 qui illustre les contributions de la variance expliquée de chaque variable sur les autres :
Une façon de considérer ce diagramme de Venne est de regarder la matrice des corrélations en prenant les variables deux par deux, ce qu’on appelle une tables d’intercorrélation :
|
Y |
Z |
|
|
X |
.25 |
.50 |
|
Y |
.35 |
Cependant, cette table ne répond toujours pas à notre question puisqu’elle continue à prendre les prédicteurs un par un. Nous souhaitons prédire Z étant donné un couple X et Y connu simultanément. Pour y arriver, nous utilisons un indice de corrélation multiple R.
4.1. Calcule du R
L’indice de corrélation multiple (pour plus de deux variables) est représenté par un R majuscule pour le différencier du cas particulier où il n’y a qu’un total de deux variables. Tout comme le r, l’indice R va de plus 1 à –1. Pour éviter les confusions, on utilise les indices tel : RZ,XYpour indiquer que l’on cherche à prédire Z à partir des valeurs simultanée de X et Y. De la même façon, R2Z,XY indique le pourcentage de la variance de Z expliqué par X et Y.
Prenons comme exemple une étude où l’on veut déterminer la relation entre la qualité des programmes qu’une personne écoute (selon son évaluation personnelle) X et le prix de son équipement Y, pour déterminer le nombre d’heure que cette personne va passer devant la télévision par semaine Z. Nous supposons que le chercheur a déjà obtenu les corrélations simples rXY , rXZ et rYZ pour chaque pair ( X, Y), ( X, Z ), et ( Y, Z ). Le R multiple se calcule comme suit :
Un coefficient de corrélation multiple s’interprète de la même façon qu’un r régulier dans le cas d’un problème à deux variables. De plus, il est aussi possible de tester des hypothèses concernant R, tel H0 : R = 0. Nous n’allons pas entrer dans les détails. Cependant, un bon logiciel d’analyse statistique va rapporter si le R obtenu est significatif ou non.
De la même façon, une droite de régression passant par les triplets de points est aussi possible. L’idée étant de prédire les Z suivant une équation de la forme :
Une chose importante à voir dans cette équation est que l’effet de X et de Y sont additifs, c’est à dire que X affecte Z indépendamment de Y. Autrement dit, ce modèle stipule qu’il n’existe pas d’interaction entre les facteurs X et Y sur la variable dépendante Z. Cet hypothèse se teste à l’aide d’une ANOVA. Si l’interaction A × B est significative, il faut simplement ne pas faire de régression multiple linéaire.
Le facteur est le ratio entre combien d’unité Z change pour chaque unité de changement dans X quand Y est tenu constant. Parce que chacun de ces coefficients représente seulement une portion de la prédiction de Z, ils sont appelés coefficients de corrélation partielle. Les équations pour calculer les pentes des effets de chaque variable individuelle sont donnés par :
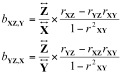
Exemple.
Soit la recherche où l’on veut déterminer la relation entre la qualité des programmes qu’une personne écoute (selon son évaluation personnelle) X et le prix de son équipement Y (en $), pour déterminer le nombre d’heure que cette personne va passer devant la télévision par semaine Z (en heures).
Le chercheur a obtenu ces trois mesures sur un échantillon de 50 personnes (non présentés). La moyenne des observations est 
= 5 (cote), 
= 205 $, 
= 18 heures.La variance (non biaisée) des observations est : 
= 2.2 (cote), 
= 88.0 $, 
= 11.8 heures. Il observe les corrélations simples rXY = .750, rXZ = .894et rYZ = .918. Il regarde en premier le coefficient de régression multiple R :
Près de 94% de la variance est expliquée quand on considère X et Y simultanément, ce qui serait significatif si on regardait un listing d’ordinateur. Les coefficients de corrélation partielle sont
Avec les valeurs moyennes, on trouve l’ordonnée à l’origine, a :
Étant données ces différentes valeurs, nous pouvons prédire le temps passé devant la télévision si le prix de la télévision X et la cote des programmes écoutés Y sont connus. Par exemple, si un individu rapporte écouter des émissions qu’il cote 3 et que son équipement coûte 100$, on s’attend à ce qu’il passe 0.076 ´ 100 + 2.51 ´ 3 –10.13 = 5 heures par semaine devant la télévision.
Exercices
1.Soi une ordonnée à l’origine de –12, une pente de 2.5. Calculez la valeur attendue de Y si X:
a)0
b)10
c)20
2. 45 sujets ont été mesurés sur 2 variables. La somme des produits des distances entre chacune de ces valeurs et leur moyenne respective est de 15975. La covariance est:
3.Quel est le pourcentage de la variance de Y expliquée par X si la corrélation est de .70.
4.La pente de régression de Y sur X étant de 0.443 et la pente de régression de X sur Y étant de 0.890, calculez le coefficient de corrélation.
5.La covariance étant de –85, la variance de X de 96, et la variance de Y 121, calculez le coefficient de corrélation.
6.Soit X = {255, 100, 307, 150} et Y = {5, 3, 6, 3},
a)Calculer les moyennes
b)Calculer les variances non-biaisées
c)Calculer la covariance
d)Calculer le coefficient de corrélation
e)La corrélation est-elle significative (a = 5%)?
f)Calculer la pente de régression
g)Calculer l’ordonnée à l’origine.
7.Soit X = {8, 12, 13, 7, 16} et Y = {3, 4, 9, 2, 12},
a)Calculer les moyennes
b)Calculer les variances non-biaisées
c)Calculer la covariance
d)Calculer le coefficient de corrélation
e)La corrélation est-elle significative (a = 5%)?
f)Calculer la pente de régression
g)Calculer l’ordonnée à l’origine.
8.Une recherche menée par un collègue vous apprend que le lien entre la variable Y et X: Y = 49 X + 3. Pouvez-vous prédire la valeur de la variable X à partir de la valeur de Y?
9.Une forte corrélation de Y sur X suggère que Y cause X?
Si vous remarquez des informations erronées ou manquantes, merci de le partager par les Commentaires.
Une réponse à «C12: Corrélation et régression»
Dans la section 3.3. La droite de régression, une erreur s'est glissée dans la première phrase (voir mot en majuscule: Soit la situation où nous observons bel et bien une corrélation significative entre un ÉCHANTILLON Y et un ÉCHANTILLON X. L’étape suivante est de quantifier la relation. Par exemple, pour chaque changement d’une unité en X, de combien change la valeur attendue en Y?). Les corrélations sont observées entre 2 variables et non entre 2 échantillons.
Tabachnick et Fidell (2007), p. 56