C10: Plans à mesures répétées
Section 1. Principes d’un plan à mesures répétées
Dans le domaine des sciences du comportement, les chercheurs utilisent souvent des humains. À cause de leurs caractéristiques personnelles, de leurs expériences, et de leurs réactivités individuelles, les réponses d’individus différents aux même traitements expérimentaux font montre d’une très grande variabilité. Dans un plan d’expérience à mesures répétées, un même sujet est mesuré sous chacun des niveaux d’un traitement expérimental. Un des principaux buts de ce plan est de permettre un meilleur contrôle des différences individuelles entre les sujets. Dans ce type de plan, l’effet de traitement de la condition i sur le sujet k est comparé avec la réponse du même sujet dans toutes les autres conditions. Dans ce plan donc, chaque sujet devient son propre contrôle à travers les différents traitements expérimentaux. Ceci permet d’éliminer de l’erreur expérimentale, la variabilité due aux différences individuelles.
L’avantage d’un plan à mesures répétées est donc important. Cependant, la difficulté augmente aussi. En effet, les termes d’erreurs ne sont pas les mêmes que pour un plan à groupe indépendant. Dans un plan p ou p × q, le terme d’erreur est toujours lié à la variance intra groupe. Par contre, dans un plan à mesures répétées, tel un plan ( p ), autant le traitement que la variabilité inter sujet se trouvent à être une variabilité intra groupe. De plus, dans un plan p × ( q ), il existe maintenant deux termes d’erreur!
Bien entendu, les principes généraux de l’ANOVA restent valides. La somme des carrés et les degrés de libertés se répartissent de façon additive. Cependant, ils ne se répartissent plus de la même façon. À la base cependant, il y a toujours une séparation intra groupe et intergroupe.
De plus, le type de test reste le même, par exemple, pour un facteur A à mesures répétées :
Rejet de H0 si![]()
La grande difficulté en fait est de bien identifier le bon terme d’erreur (le dénominateur) et le bon nombre de degrés de liberté. Au cours 9, section 3 (suite), nous avons illustré la décomposition de la somme des carrés et des degrés de liberté pour tous les plans possibles à un ou deux facteurs.
Dans ces diagrammes, les termes d’erreurs sont tous reliés à de la variabilité liée aux participants de l’expérience. On note donc toujours cette variabilité par SCS|??.
1.1. Plan (p)
Dans un plan à mesures répétées, on cherche à vérifier des hypothèses sur les différences de moyennes obtenues par un seul groupe de n sujets. Ce groupe est soumis à p traitements expérimentaux et les sujets, mesurés sur une variable dépendante.
Exemple.
Un chercheur veut évaluer l’effet de quatre médicaments sur le temps de réaction des patients dans une série de tests classiques. Cinq sujets différents participent à l’expérience et la performance de chacun est mesurée sous l’effet de chaque médicament, l’ordre d’administration étant réparti de façon aléatoire et avec un délai suffisant entre chacun. La variable dépendante est le temps de réaction moyen en dixième de secondes aux différentes tâches.
|
Médicaments |
|||||
| sujet | 1 | 2 | 3 | 4 | moyenne |
| 1 | 16 | 28 | 30 | 34 | 27 |
| 2 | 10 | 18 | 14 | 22 | 16 |
| 3 | 18 | 20 | 24 | 30 | 23 |
| 4 | 20 | 34 | 38 | 44 | 34 |
| 5 | 14 | 28 | 26 | 30 | 24.5 |
| moyenne | 15.6 | 25.6 | 26.4 | 32.0 | 24.9 |
Ici, chaque ligne représente un sujet, le même à travers toutes les conditions. Pour cette raison, on fait une moyenne du sujet. Par exemple, on note que le sujet 4 est systématiquement plus lent et le sujet 2 systématiquement plus rapide. Sachant cela, les calculs de l’ANOVA à mesures répétées vont ignorer cette source de variabilité, chose qu’il n’est pas possible de faire dans un plan à groupes indépendants puisque les sujets ne sont mesurés qu’une fois.
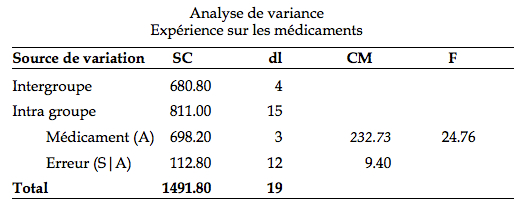
La ligne intergroupe rapporte la variabilité du sujet en moyenne par rapport à la moyenne des moyennes (est-ce un sujet rapide? lent?). Cette information n’est pas utilisée dans la suite. On utilise un seuil de 1%. L’hypothèse nulle est :
H0 : μ1 =μ2 =μ3 =μ4
Le test est du genre
Rejet de H0 si![]()
La valeur critique pour un test F avec (3, 12) degrés de liberté est 5.95. Comme on le voit, il existe au moins une différence significative entre la moyenne inférieure (Médicament 1: 15.6) et la moyenne supérieure (Médicament 4: 32.0)
Juste pour illustrer l’avantage du plan à mesures répétées, imaginons que le chercheur aurait mal fait son analyse, indiquant au logiciel que le facteur A est un facteur à groupe indépendant. La même somme des carrés pour le facteur A aurait été trouvé (698.20). Cependant, le terme d’erreur aurait regroupé autant le terme d’erreur S|A que la variance intergroupe (SCinter + SCS|A = 680.80 + 112.80 = 793.60). Le tableau d’ANOVA aurait alors été du genre :
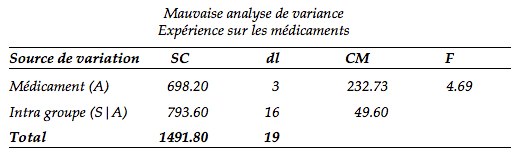
La valeur du ratio n’est pas supérieure à la valeur critique. On ne peut donc pas rejeter l’hypothèse nulle. Selon cette mauvaise analyse, il n’existe aucune différence entre 32.0 et 15.6! Cette décision erronée vient du fait que s’il s’agit de groupes indépendants, ils sont très variables. Par exemples, les scores du « groupe » 3 vont de 14 à 38. La variabilité due au traitement n’excède pas cette variabilité intra groupe. Cependant, sachant que ce sont les mêmes sujets, la variabilité entre les sujets est évacuée dans la somme des carrés inter groupe (ici, on serait mieux de lire inter sujet) qui est très grande (680.80).
Si jamais le chercheur veut en savoir plus sur ce qui se passe pour les deux autres médicaments, il peut procéder à une comparaison des moyennes.
Le test pour la comparaison des moyennes individuelles est :
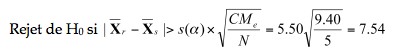
La valeur critique s(a) est donnée en fonction des degrés de liberté (4, 12) car il y a quatre moyennes à comparer. Au seuil de 1%, on obtient la valeur 5.50. Donc, toute différence supérieure à 7.54 est significative.
| Différences | 2 | 3 | 4 |
| 1 | 10.0** | 10.8** | 16.4** |
| 2 | 0.8 | 6.4 | |
| 3 | 5.6 | ||
| ** : p < .01 | |||
Ainsi, le médicament 1 diffère de tous les autres médicaments et réduit le plus les temps de réponse. Les trois autres médicaments sont similaires, ralentissant également les performances.
1.2. Plan p×(q)
Ce type de plan factoriel est aussi appelé un plan mixte car il intègre des mesures répétées et des groupes indépendants. Ce type d’expérience manipule deux facteurs, A et B, ayant respectivement p et q niveaux en étudiants p groupes indépendants de sujets mesurés dans q conditions.
Dans un plan p × ( q ), il existe deux sources d’erreur, SCS|AB et SCS|A. Il faut toujours utiliser le terme d’erreur de même catégorie (intra groupe ou intergroupe) que l’effet testé. Ainsi, l’effet B et l’effet d’interaction A ´ B sont testés suivant le même terme d’erreur intra groupe.
Exemple.
Supposons une expérience en ergonomie effectuée pour le compte du ministère du transport dont le but est d’évaluer l’efficacité dans les avions de lignes de trois types d’avertisseurs de décrochage. Le facteur A désigne la modalité de présentation des signaux : a1 = visuel, a2 = auditif, a3 = auditif et visuel. Le facteur B désigne les niveaux de fatigue des pilotes, soit b1 = 1 heure de vol, b2 = 2 heures, b3 = 3 heures. La performance des pilotes est mesurées en utilisant des simulateurs de vol dans des situations d’urgences durant lesquelles l’attention est concentrées sur des tâches distrayantes. La variable dépendante est le nombre d’erreur de détection. Quinze pilotes d’expérience et de compétence équivalentes sont divisés en trois groupes de 5 sujets, un groupe pour chaque modalité de présentation. Il s’agit donc d’un plan 3 × ( 3 ) à mesures répétées sur le niveau de fatigue.
|
Moments (B) |
|||||
| Modalité (A) | 1 hre | 2 hre | 3 hre | ||
| Visuel | 7, 6, 9, 10, 11 | 8, 8, 10, 11, 13 | 9, 12, 13, 14, 15 | ||
| Auditif | 2, 2, 3, 7, 6 | 4, 6, 7, 9, 9 | 7, 10, 10, 11, 12 | ||
| Auditif + visuel | 3, 3, 4, 8, 7 | 4, 6, 7, 8. 10 | 7, 9, 9, 10, 10 | ||
Dans le tableau des données brutes, chaque ligne représente un même sujet dans trois situations de fatigue. Les moyennes sont :
| Moments | ||||
| Mode | 1 hre | 2 hre | 3 hre | Moyenne |
| Visuel | 8.60 | 10.00 | 12.60 | 10.40 |
| Auditif | 4.00 | 7.00 | 10.00 | 7.00 |
| Auditif+Visuel | 5.00 | 7.00 | 9.00 | 7.00 |
| Moyenne | 5.87 | 8.00 | 10.53 | 8.78 |
Le tableau de l’ANOVA est :
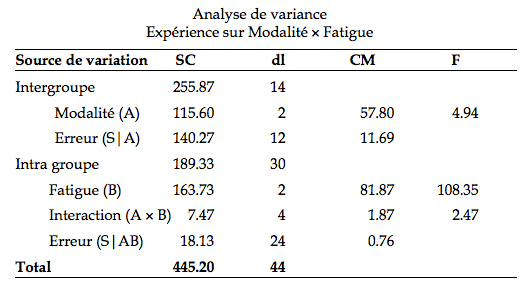
Au niveau α = .05, la valeur critique pour l’interaction est de 2.776 avec (4,24) degrés de libertés, et pour les effets principaux, 3.885 et 3.403 pour (2, 12) et (2, 24) degrés de libertés respectivement.
L’interaction A × B n’est pas significative (F(4, 24) = 2.47, p > .05). On peut donc interpréter directement les effets principaux sans recourir aux effets simples. L’effet de la modalité est significatif (F(2, 12) = 4.94, p < .05). La modalité visuelle entraîne significativement plus d’erreur de détection que les deux autres modalités (étant strictement égaux, on peut les comparer ensemble). De plus, le niveau de fatigue a aussi un effet significatif sur le nombre d’erreur (F(2, 24) = 108.35, p < .05). Les erreurs de détection sont significativement plus nombreuses après trois heures de pilotage qu’après 1 heure.
Une comparaison de moyenne suivant la méthode de Tukey montre aussi que les erreurs de détection après deux heures de pilotage sont significativement plus nombreuses qu’après une heure mais significativement moins qu’après trois heures de pilotage.
Pour s’en assurer, le test pour la comparaison des moyennes individuelles est :
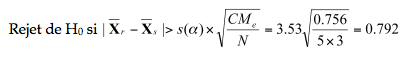
La valeur critique s(a) est donnée en fonction des degrés de liberté (3, 24) car il y a trois moyennes à comparer. Au seuil de 5%, on obtient la valeur 3.53. Donc, toute différence supérieure à 0.792 est significative.
| différences | 2 | 3 | |
| 1 | 2.13* | 4.66* | |
| 2 | 2.53* | ||
| * : p < .05 | |||
1.3. Plan (p x q):
Le plan factoriel ( p × q ) est un plan d’expérience comportant deux facteurs A et B ayant respectivement p et q niveaux. Dans ce plan, il n’y a qu’un seul groupe de n sujets qui est mesuré p ´ q fois.
Dans un plan ( p × q ), il existe trois termes d’erreurs. Ils sont tous intra groupe, tout comme les effets A, B, et A ´ B. On prend le terme d’erreur regroupant la variabilité résiduelle à l’effet testé SCS|A, SCS|B, et SCS|AB pour les effets A, B, et A ´ B respectivement.
Exemple.
Soit une recherche hypothétique ayant comme plan un ( 2 × 4 ). L’échantillon comporte un groupe de 5 sujets mesurés dans 8 conditions différentes. Les données brutes sont :
|
Facteur A |
|||||||
|
a1 |
a2 |
||||||
|
Facteur B |
Facteur B |
||||||
|
b1 |
b2 |
b3 |
b4 |
b1 |
b2 |
b3 |
b4 |
|
3 |
5 |
6 |
9 |
8 |
6 |
7 |
11 |
|
7 |
11 |
11 |
12 |
10 |
12 |
13 |
9 |
|
9 |
13 |
12 |
14 |
10 |
15 |
14 |
8 |
|
4 |
8 |
7 |
11 |
8 |
9 |
9 |
7 |
|
1 |
3 |
4 |
5 |
10 |
5 |
7 |
9 |
Les moyennes sont :
|
Facteur B |
|||||
| Facteur A | b1 | b2 | b3 | b4 | moyenne |
| a1 | 4.8 | 8.0 | 8.0 | 10.2 | 7.8 |
| a2 | 9.2 | 9.4 | 10.0 | 8.8 | 9.4 |
| moyenne | 7.0 | 8.7 | 9.0 | 9.5 | 8.6 |
Le tableau d’ANOVA est :
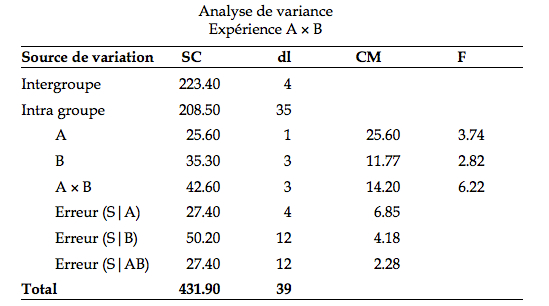
Au niveau α = .05, la valeur critique pour l’interaction est de 3.490 aux degrés de libertés (3, 12).
l’interaction A × B est significative (F(3, 12) = 6.22, p < .05). Si vous faîtes le graphique, vous voyez qu’en effet, les lignes ne sont pas parallèles. Pour avoir un meilleur portrait, nous passons aux effets simples. Puisque A n’a que deux niveaux, en faisant les effets simples de A pour chaque niveau de la variable B, nous allons en fait comparer des couples de moyennes. Si ces couples diffèrent, nous n’aurons pas besoin d’utiliser la technique de Tukey.
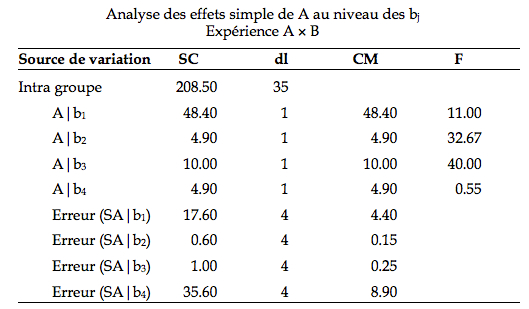
La valeur critère est de 7.709 pour (1, 4) degrés de liberté. Comme on le voit, les moyennes au niveau de b1 diffèrent significativement (F(1, 4) = 11.00, p< .05). Il en va de même pour les moyennes aux niveaux de b2 et de b3 (F(1, 4) = 32.67 et 40.00 respectivement, p < .05) Par contre, au niveau b4, les moyennes ne diffèrent pas entre elles.
Section 2. Le correctif de Greenhouse-Geisser
Un des postulats sous-jacent à l’ANOVA dans un plan à mesures répétées est celui de l’homogénéité des variances (voir aussi le cours suivant). Si ce postulat n’est pas respecté, le test F devient un test biaisé. Greenhouse et Geisser (1958) ont élaboré une méthode pour corriger ce biais en ajustant à la baisse le nombre de degrés de liberté des effets à mesures répétés de façon à rendre le test plus conservateur. Le correctif de Greenhouse-Geisser (GG) n’exige aucun calcul supplémentaire sauf pour les nouveaux degrés de liberté. En règle générale, les logiciels calculent automatiquement les F corrigés par la méthode GG.
Dans l’analyse et l’interprétation des résultats, il faut donc tenir compte des éléments suivants :
- Si le test F conventionnel et le test F corrigé par la méthode GG sont tous deux non-significatifs au seuil a, on ne peut rejeter H0.
- Si le test F conventionnel et le test F corrigé par la méthode GG sont tous deux significatifs au seuil a, on rejette H0.
- Si le test F conventionnel est significatif mais pas le test F corrigé par la méthode GG, on doit interpréter les résultats avec nuances et réserve ou alors utiliser une méthode statistique multivariée (qui tient compte de la covariance dans les données) tel le T2 de Hotelling qui permet une évaluation plus exacte de la probabilité de rejet de H0.
Section 3. Répartition des écarts au carré dans les plans simples p ou (p)
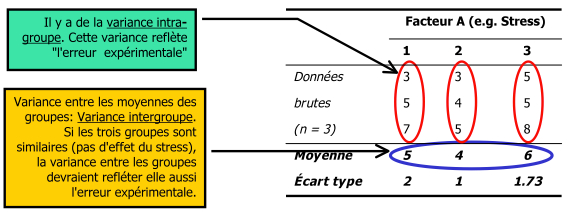
Cette section récapitule la répartition des écarts au carré dans le but d’avoir une meilleure intuition de ce qu’on entend par variance intergroupe et intra groupe. L’idée générale est de maximiser l’information soutirée par les moyennes marginales. La somme des écarts au carré total est toujours obtenue en regardant les écarts entre les données brutes et la moyenne des moyennes.
3.1. Plan à groupes indépendants
Nous utilisons l’indice k pour le niveau du traitement et i pour le numéro du sujet.
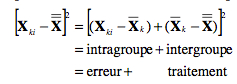
La Figure 1 montre cette répartition.
3.2. Plan à mesures répétées
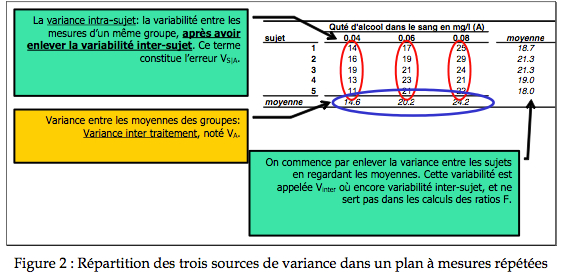
La particularité ici est que se sont toujours les mêmes sujets d’un niveau à l’autre du traitement. Nous pouvons donc profiter du fait que nous avons une moyenne pour chaque sujet. Les écarts entre les sujets et la moyenne des sujets représentent donc une variabilité entre les individus qui est normale et peu informative. On l’appelle la variabilité inter-sujet. Nous l’évacuons de la somme des carrés dès le début du calcul, et ne l’utilisons jamais.
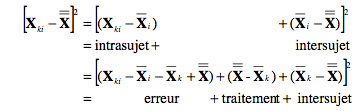
La Figure 2 montre ces trois sources de variances.
Exercices
1.Soit ce tableau d’: Analyse de variance Expérience A × B
| source de variation |
SC |
dl | CM | F |
| A | 25.6 | 1 | 25.6 | 3.7 |
| B | 35.3 | 3 | 11.7 | 2.8 |
| A ´ B | 42.6 | 3 | 14.2 | 6.2 |
| Erreur (S|A) | 27.4 | 4 | 6.8 | |
| Erreur (S|B) | 50.2 | 12 | 4.1 | |
| Erreur (S|AB) | 27.4 | 12 | 2.2 | |
| Total | 431.9 | 35 |
- De quel type de plan s’agit-il?
- Faîtes un graphique des moyennes cohérent avec ces résultats
2.Si je rajoute ces effets simples à la question précédente, pouvez-vous raffiner le graphique des moyennes?
Analyse des effets simples de A au niveau des bdans l’expérience A ´ B
| source de variation |
SC |
dl | CM | F |
| A|b1 | 48.4 | 1 | 48.4 | 11.00 |
| A|b2 | 4.9 | 1 | 4.9 | 32.67 |
| A|b3 | 10.0 | 1 | 10.0 | 40.00 |
| A|b4 | 4.9 | 1 | 4.9 | 0.55 |
| Erreur (SA|b1) | 17.6 | 4 | 4.4 | |
| Erreur (SA|b2) | 0.6 | 4 | 0.15 | |
| Erreur (SA|b3) | 1.0 | 4 | 0.25 | |
| Erreur (SA|b4) | 35.6 | 4 | 8.90 |
Finalement, si je vous donne ces parcelles d’interprétation, pouvez-vous faire un graphique reproduisant parfaitement les moyennes obtenues dans cette expérience A ´ B? « Au niveau de b1, Le premier niveau de A est significativement supérieur au second niveau. Pour les niveaux 2 et 3, l’inverse est vrai. »
Si vous remarquez des informations erronées ou manquantes, merci de le partager par les Commentaires.


