Section 1. Régularité de la nature et effets linéaires

La recherche de lois scientifiques passe la découverte de régularités. La meilleure façon est de faire des mesures quand un facteur varie suivant plusieurs niveaux. Lorsqu’un graphe des résultats montre une ligne parfaitement droite, on sait qu’on vient de découvrir une régularité. Dans les faits cependant, il est rare d’obtenir des effets linéaires, surtout en psychologie. En physique, Newton a révolutionné le monde en mettant en évidence un effet linéaire de l’accélération sur la force, F(a) = m × a. De la même façon au début du XX^ième siècle, l’effet photo-électrique était très déroutant jusqu’à ce que Einstein en 1905 trouve une façon de regarder les résultats tel que l’effet photo-électrique était parfaitement linéaire. De façon générale, découvrir une relation linéaire entre un facteur et une mesure est la meilleure indication qu’il existe une régularité, surtout si l’effet se maintient lorsque l’expérience est répétée. Quand l’effet n’est pas linéaire, une façon de vérifier que l’effet est bien réel est de voir si la courbe du graphe ne peut pas être transformée de telle façon que l’effet résultant forme une ligne droite. Ce faisant, le chercheur démontre la régularité de façon frappante, et en plus, il montre quelle peut bien être la forme de la courbe avant transformation. La recherche de lois scientifiques passe la découverte de régularités. La meilleure façon est de faire des mesures quand un facteur varie suivant plusieurs niveaux. Lorsqu’un graphe des résultats montre une ligne parfaitement droite, on sait qu’on vient de découvrir une régularité. Dans les faits cependant, il est rare d’obtenir des effets linéaires, surtout en psychologie. En physique, Newton a révolutionné le monde en mettant en évidence un effet linéaire de l’accélération sur la force, F(a) = m × a. De la même façon au début du XX^ième siècle, l’effet photo-électrique était très déroutant jusqu’à ce que Einstein en 1905 trouve une façon de regarder les résultats tel que l’effet photo-électrique était parfaitement linéaire. De façon générale, découvrir une relation linéaire entre un facteur et une mesure est la meilleure indication qu’il existe une régularité, surtout si l’effet se maintient lorsque l’expérience est répétée. Quand l’effet n’est pas linéaire, une façon de vérifier que l’effet est bien réel est de voir si la courbe du graphe ne peut pas être transformée de telle façon que l’effet résultant forme une ligne droite. Ce faisant, le chercheur démontre la régularité de façon frappante, et en plus, il montre quelle peut bien être la forme de la courbe avant transformation.
En psychologie, une loi importante est la loi de l’apprentissage. Cependant, il ne s’agit pas d’un effet linéaire: En début d’apprentissage, les participants apprennent très vite à faire mieux (moins d’erreur ou réponses plus rapides, selon ce que le chercheur mesure). Par contre, au fur et à mesure que les participants approchent de leur plancher, l’amélioration se fait de plus en plus lentement. L’ensemble forme une courbe du genre:
Newell et Rosenbloom ont montré en 1981 la régularité de cette courbe en trouvant une transformation des axes qui rende la courbe parfaitement linéaire et ont montré sur une cinquantaine d’ensembles de données obtenus sur une grande variété de tâches très différentes les unes des autres (tel le temps pour rouler un cigare, le temps pour trouver Charlie, le nombre d’erreur de multiplication, etc.) qu’à chaque fois, la courbe devenait très linéaire. Ils ont été les premiers à détecter « la loi d’apprentissage ».

Section 2. Homogénéité des variances

Un postulat important à la base de l’ANOVA concerne l’homogénéité des variances. Plusieurs études semblent démontrer que dans le cas d’échantillons d’effectifs égaux, le test F est un test robuste, c’est à dire qu’il est peu affecté par la violation du postulat de normalité des données brutes et la violation de l’homogénéité des variances. C’est une des raisons pour laquelle plusieurs auteurs recommandent fortement l’utilisation de groupes égaux. Toutefois, Wilcox (1987) démontre que même dans le cas d’échantillons de tailles égaux, le test F peut être affecté par une hétérogénéité sévère des variances, d’où l’importance d’une vérification préalable à l’aide de tests statistiques.
Conover et al. (1981) ont recensé et comparé 56 tests d’homogénéité des variances. Un des meilleurs est le test de Levene (1960) et sa variante, le test de Brown-Forsythe (1976).
Le test de Levene consiste à utiliser une analyse de variance simple sur des valeurs Z_ki qui sont la distance de chaque donnée brute X_ki à la moyenne de son groupe _i. Comme on soustrait la moyenne, toutes les valeurs Z_ki ne devraient refléter que la variance autour de zéro. S’il existe encore un effet du traitement, cela signifie que la variance n’est pas également répartie entre les conditions.
Formellement

Z_ki = | X_ki – _i|

H₀ : s²₁ =s²₂ =… =s²_p

Le rejet de l’hypothèse nulle (un ratio F significativement supérieur à 1.00) implique la présence d’hétérogénéité dans les variances et la nécessité de recourir à une transformation non linéaire des données dans le but de ramener les scores extrêmes plus près de la moyenne.
Une variante du test de Levene est le test de Brown-Forsythe. Elle consiste à soustraire la médiane dans chaque condition plutôt que la moyenne.
Malheureusement, ces deux tests ne sont pas réalisés automatiquement par le logiciel SPSS. Il faut donc soit écrire un programme qui va calculer les Z_ki avant de faire une ANOVA usuelle, ou alors utiliser les autres tests incorporés dans le logiciel SPSS.
Ces tests alternatifs sont le test de Cochrans et le test de Bartlett.

Section 3. Restauration de l’homogénéité des variances

N’importe quelle transformation non linéaire peut être réalisée sur les données brutes. Cependant, il faut savoir quel est votre objectif avant de procéder.
Si l’hypothèse d’homogénéité des variances est rejetée, il est nécessaire d’effectuer l’une des transformations suivantes qui aura pour effet de normaliser les distributions, soit de rendre les variances plus comparables entre les conditions. Notons qu’une transformation est très facile à réaliser avec la plupart des logiciels d’analyses statistiques.

3.1. Transformation par la racine carrée
Cette transformation implique de changer les X_ki ainsi :

Elle est souvent utile lorsque la variable dépendante est une fréquence, par exemple, le nombre d’erreurs, le nombre de réponses, etc.

3.2. Transformation logarithmique
Cette transformation est parfois utilisée lorsque la variable dépendante est mesurée en unité de temps, par exemple, secondes, minutes, etc. Cette transformation a pour effet de stabiliser la variance et de normaliser les distributions qui ont une asymétrie positive. Elle s’obtient avec la transformation suivante

3.3. Transformation angulaire
Dans une expérience, il arrive souvent que la variable dépendante soit exprimée en pourcentage, ce qui se produit par exemple lorsqu’on mesure le nombre de bonnes réponses sur un maximum possible. Dans ce cas, si les variances sont hétérogènes, il faut procéder à une transformation angulaire de la forme :

Dans ce cas, X’ devient une mesure exprimée en radians. La variable X doit être incluse entre 0 et 1, sinon la transformation donnera des résultats aberrants.

Section 4. Restauration de la linéarité dans le cas d’effets courbes

Dans un grand nombre d’expérience, on utilise des niveaux qui s’accroissent continûment, suivant une échelle de type II. Dans ces cas, la relation devient très facile à analyser (comme on le verra aussi au cours 12), et la pente de la droite a une signification directe. Par exemple, supposons une expérience de recherche visuelle. Dans cette expérience, on montre à un sujet une scène contenant 1, 2, 3, … objets, et le sujet doit décider aussi rapidement que possible si un objet précis (la cible) est présent. L’exemple par excellence se trouve dans les livres « Où est Charlie ». Le graphe suivant illustre le type de données que l’on peut obtenir dans un plan à 4 mesures répétées sur le nombre d’objets (1 à 4).

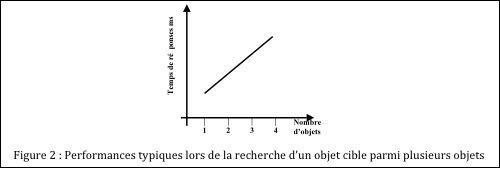
Dans ce cas, la pente de la fonction nous indique le temps qu’il faut pour traiter chaque objet supplémentaire. Il s’agit donc d’une indication du mouvement de l’attention.
À l’occasion, on obtient des effets qui, sans être linéaires, semblent doté d’une régularité très précise. Par exemple, on peut étudier le temps qu’il faut pour décider si deux objets successifs sont identiques ou différents. On trouve que le temps pour dire « identique » s’accroît avec la complexité des objets, comme on le voit sur le panneau de gauche de la Figure 3. Cependant, l’accroissement n’est pas linéaire, mais forme plutôt une courbe concave. Dans ces cas, pour voir si la relation est vraiment stable plutôt que simplement illusoire, on peut faire un graphe de type log-log

Comme on le voit sur le panneau de droite de la Figure 3, avec un graphe log-log, les données sont parfaitement linéaires, ce qui suggère que la courbe empirique obtenue à gauche n’est pas farfelue ou résultante du hasard.
Utiliser un graphe de type log-log revient à transformer les données brutes X_ki et les niveaux a_i. La relation est simplement a’_i = Log(a_i) et X’_ki = Log(X_ki). Ce genre de transformation est souvent utilisé en ingénierie, et commence à l’être en psychologie, notamment en perception, où il semble exister un grand nombre de lois très stables, mais non linéaires.
Un autre exemple concerne la loi d’apprentissage. Il semble bien établi que les performances s’améliorent avec la pratique suivant une équation du type: En psychologie, une loi importante est la loi de l’apprentissage. Cependant%2

Perf(N) = a + b N^-c

où Perf mesure la performance après N heures d’entraînement, et a, b, c sont les paramètres du sujet. Souvent, Perf est le temps pris pour compléter une tâche, temps qui se réduit avec la pratique. La courbe ressemble à celle du panneau de gauche de la Figure 4 qui devient linéaire sur un graphe de type log-log, comme on le voit sur le panneau de droite de la Figure 4.

Exercices

1.Soit les données de la Figure 5 (fictives) représentant des taux d’erreur d’un participant dans deux tâches différentes en fonction du nombre d’heure d’entraînement (première colonne):

a) Est-ce que les effets sont linéaires dans la tâche 1 (colonne 2)? dans la tâche 2 (colonne 3). Pour répondre à la question, faites un graphe des moyennes.
b) Calculer dans deux autres colonnes le log (ln) du taux d’erreur dans la tâche 1, dans la tâche 2. Est-ce que l’effet devient linéaire en fonction de session? Si oui, quel type de graphe avez-vous fait?
c) Calculer dans une dernière session le log du nombre d’heure d’entraînement. Est-ce que l’effet devient linéaire en fonction de Log(session)? Si oui, quel type de graphe avez-vous fait?

Show Press Release (62 More Words)

Les données de la tâche 2 deviennent linéaires en fonction du nombre d’heure d’entraînement lorsque transformées avec le log. Il s’agit d’un graphe log-linéaire, souvent utilisé en ingénierie, et suggère une relation exponentielle. Les données de la tâche 2 deviennent linéaires en fonction du log(nombre d’heure) lorsque transformée avec le log. Il s’agit donc d’un graphe log-log, souvent utilisé en psychologie cognitive.