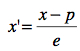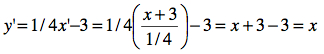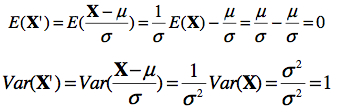C3 : Probabilités
Section 1. La roulette russe: problème empirique?
La probabilité est apparue dans les années 1600, époque où les jeux de hasard étaient très prisés. Avant de faire un pari, l’aristocrate moyen voulait connaître ses chances de gagner. Or, ils ne connaissaient d’autres moyens de faire ce calcul que de jouer le jeu un grand nombre de fois avec un serviteur de confiance. La probabilité de gagner devient:
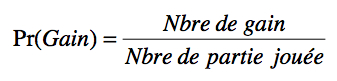
(Vous comprendrez que cette méthode n’était guère utile au jeu de la roulette russe). Pour contrer cette stratégie fort simple, certains joueurs inventèrent des jeux plus complexes, souvent basés sur une séquence. Pour évaluer leur chance, certains aristocrates n’eurent d’autres recours que d’aller consulter les plus grands mathématiciens de leurs temps (les Bernoulli, Pascal, Fermat, etc.). Ces derniers firent bien plus qu’évaluer les chances de gain, ils établirent les probabilités de voir tel ou tel événement se produire dans une situation donnée très générale. Nous examinons quelques-unes de ces distributions de probabilité dans la suite.
Section 2. Rôle de la probabilité en statistiques inductives
La probabilité est la branche des mathématiques qui s’occupe des populations. Étant donnés quelques postulats simples, peut-on savoir comment les scores de la population entière seront répartis. Idéalement, on souhaite avoir le moins de postulats possibles (dans le but d’une plus grande généralité).
On peut voir les probabilités comme une grosse expérience de pensée : Peut-on, par la seule logique, prédire le résultat d’une « expérience ». Par exemple, imaginons qu’une
« expérience » consiste à lancer 10 fois une pièce de monnaie. Peut-on prédire d’obtenir 8 fois pile? Sans les mathématiques, nous sommes contraints de nous fier à notre intuition, à notre expérience. Dans ce cas-ci, notre intuition suggère que c’est sans doute très rare. Or, les mathématiciens (Bernoulli le premier) peuvent nous dire la probabilité exacte que cela se produise sans même avoir jamais lancé une pièce de monnaie de leur vie. Le résultat, nous le verrons à la section 3, est d’un peu moins de 5%.
La démarche des probabilités consiste toujours par poser des postulats : « Et si… » et de voir quelles conséquences on peut en tirer. Par exemple, « Et si je connaissais la probabilité d’un pile lors d’un lancé unique, pourrais-je en déduire la probabilité d’obtenir r piles sur n lancés? ». Comme les postulats sont souvent généraux, les conséquences trouvées peuvent aussi servir dans d’autres situations. Par exemple, la question « Si j’ai 10 enfants, quelle est la probabilité d’en avoir 8 avec les yeux bleus? » nécessite exactement le même raisonnement mathématique que celui avec les pièces de monnaie pour être résolue.
L’idée générale d’introduire les probabilités en statistiques sera plus claire au cours suivant sur la statistique inductive, dans laquelle l’on souhaite déduire des informations sur une population à partir d’informations sur un échantillon.
Section 3. La distribution binomiale
La distribution la plus simple est celle qui décrit des événements n’ayant que deux possibilités. Par exemple, une pièce de monnaie est lancée, et le résultat peut être pile ou face. Ou encore, un individu est choisi au hasard et son sexe est noté. Le résultat peut être Homme ou Femme. Dans l’industrie, une machine peut fonctionner ou être en panne, etc. Un essai où seulement deux cas sont possibles est parfois appelé un essai de Bernoulli, en l’honneur du mathématicien qui le premier a travaillé ce genre de problème au cours des années 1700.
En général, l’un des deux résultats est appelé de façon arbitraire un « succès » et l’autre un « échec ». Pour simplifier, notons p la probabilité d’un succès, Pr{S}. Il s’ensuit que 1 – p est la probabilité d’un échec, Pr{E} (souvent, les auteurs notent 1 – p en utilisant la lettre q). Dans le cas d’une pièce de monnaie non truquée, p = 1⁄2. Dans le cas de la machinerie, l’entrepreneur souhaite que p soit le plus élevé possible.
3.1. Calculer la probabilité d’un nombre de succès r.
Dans un essai de Bernoulli, chaque essai est indépendant des essais précédents. Il découle alors que la probabilité est simplement multiplicative. Par exemple, la probabilité de deux succès est Pr{S, S} : Pr{S, S} = Pr{S} × Pr{S} = p × p = p2. Ainsi, Pr{S, S, E, S, E, E} = p ×p × (1-p) × p × (1-p) × (1-p) = p3 (1-p)3. Notez qu’en fait, l’ordre dans lequel les résultats sont obtenus n’est pas important puisqu’ils sont indépendants.
Si, au lieu d’être intéressé dans le résultat d’un seul évènement, nous souhaitons quantifier le nombre total de succès, par exemple, le nombre de machines défectueuses dans une usine, nous devons tenir compte du nombre de façons possibles d’obtenir ce résultat donné. Par exemple, au cours d’une joute où on lance cinq fois une pièce de monnaie, on veut savoir la probabilité d’obtenir 3 piles (P). On peut obtenir ce résultat de l’une ou l’autre de ces façons :
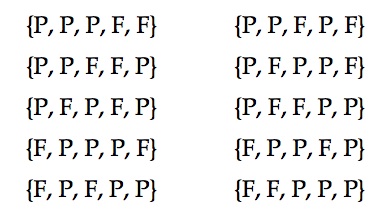
Soit 10 façons différentes d’obtenir 3 piles parmi 5 lancés. La probabilité d’obtenir le premier résultat est de p3 (1 – p)2. De même la probabilité d’obtenir la seconde configuration, etc. Donc, la probabilité d’obtenir un total de 3 piles parmi 5 lancés, peu importe l’ordre, est de 10 p3 (1 – p)2. De façon générale, il faut toujours multiplier la probabilité d’une configuration par le nombre de façons de l’obtenir. Pour cette raison, on utilise l’opérateur 
qui indique le nombre de combinaisons possibles de r parmi n événements binaires. On calcule ce nombre avec la formule
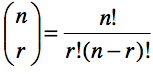
Quand une variable est le résultat d’un événement aléatoire du genre d’un essai de Bernoulli, on dit que X reflète une distribution binomiale. Pour simplifier, on peut écrire plus densément qu’une variable aléatoire X est le nombre de succès obtenus dans une suite de n essais de Bernoulli, au cours desquels la probabilité d’un succès est p à l’aide de la notation: X ~ B(n, p). Dans ce cas, la probabilité d’avoir r succès au cours de n essais, Pr{ Xi = r succès} est donné par
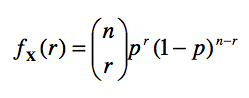
3.2. Paramètre et fonction de masse
Ce que l’on doit retenir de ce qui précède est que si l’on a des postulats simples sur une population (ici des événements binaires, chacun avec une probabilité p et 1 – p) alors il est possible d’obtenir la probabilité pour chaque observation possible (obtenir 0 succès : f (0), obtenir 1 succès : f (1), etc.). Cependant, en plus de ces postulats sur notre population, il est nécessaire de connaître les valeurs p et n. On appelle ces valeurs des paramètres de la population. En probabilité, p et n sont données. Par contre, comme on le verra dans le cours 4, en statistique, ces valeurs sont généralement des inconnues que l’on essaie d’estimer avec des échantillons. La fonction f(r) est la fonction de masse (PDF, voir lexique) qui décrit les probabilités pour tous les r. Comme on le verra au point c, il n’en faut pas plus pour calculer les moments statistiques d’un point de vue purement théorique.
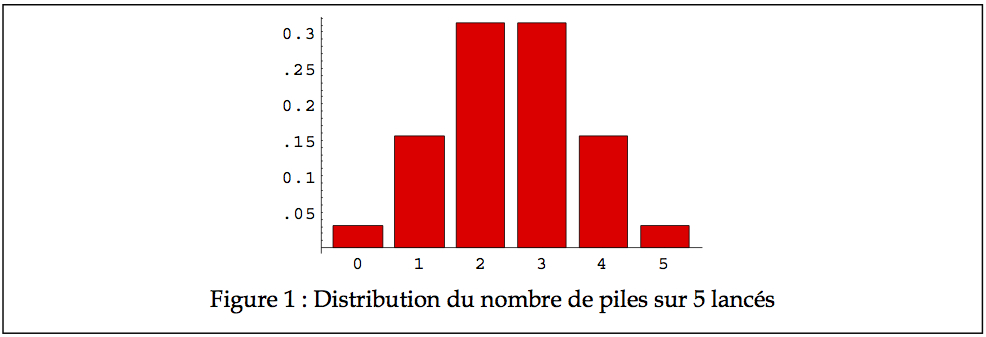
Pour vous pratiquer, essayez de calculer à la main la probabilité d’obtenir 0 pile sur 5 lancés d’une pièce de monnaie, 1 pile, etc. Puisque ces nombres représentent une fréquence relative, on peut faire un graphique des histogrammes, qui devrait alors ressembler à celui de la Figure 1.
Dans le cas où p est 1⁄2, on observe une distribution symétrique avec une moyenne qui semble être à 2.5. Cependant, p n’est pas toujours de 1⁄2. Dans le cas de machineries industrielles, la probabilité p qu’une machine soit en panne peut être de l’ordre de 1/100. Quelle est la probabilité que l’on trouve trois machines en panne au même moment dans une usine de 35 machines? Le graphique de la Figure 2 illustre ces probabilités (manque les histogrammes de 11 à 35, mais ils sont virtuellement de zéro).
Comme on le voit, la probabilité que le nombre de pannes soit de 5 est excessivement
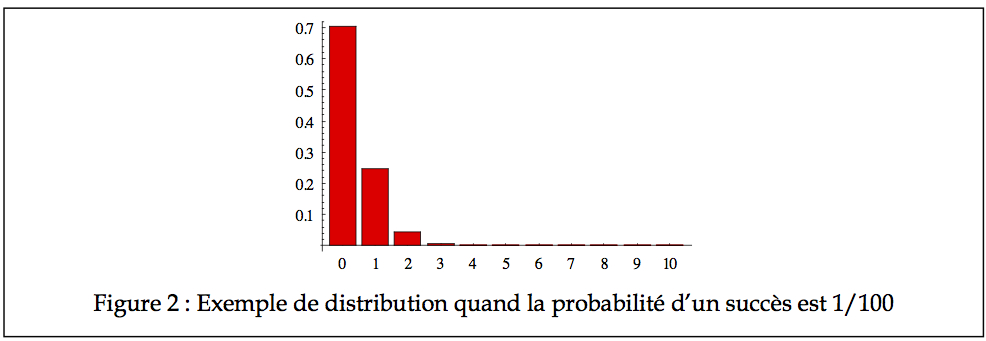
faible (de l’ordre de 4 × 10-4). Avec un tableau cumulatif (graphe des fréquences cumulatives ou CDF), on voit bien que tous les nombres de pannes probablement possibles se situent entre 0 et 2, comme on le voit à la Figure 3.
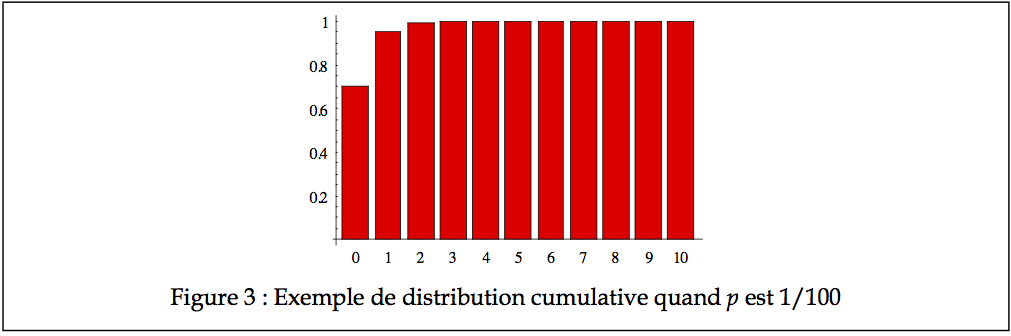
Dans ce dernier cas, l’asymétrie est extrême (et positive), et le nombre modal de panne est zéro. La moyenne est de 0.35 panne, soit moins de une en moyenne. Si vous voulez calculer la moyenne à la main dans ce dernier cas, vous allez trouver l’exercice assez laborieux. Il est cependant possible de résumer les moments statistiques à l’aide de formules simples, comme nous le montrons ici.
3.3. Calcul des moments statistiques.
a. Calcul de la moyenne d’une variable aléatoire de type binomial
On peut calculer la moyenne attendue de X, notée ici E(X) en utilisant la formule du cours 2.1: E(X)= sum{r=0}{n}{} r f(r) où r dénote tous les résultats possibles pour X (soit 0 succès, 1 succès, … n succès). Pour y arriver, il faut connaître ces relations :
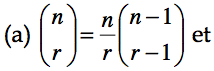
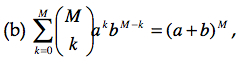
Notons qu’avec la relation (a), nous pouvons récrire :
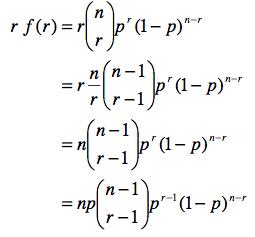
Dès lors, on peut écrire :
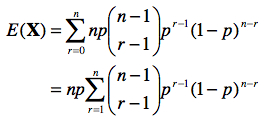
Si nous posons k = r – 1 et M = n – 1, nous obtenons :
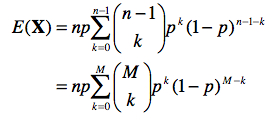
que l’on peut résoudre à l’aide de la relation (b) en posant a = p et b = (1-p) :
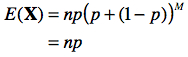
b. Calcul de la variance d’une variable aléatoire binomiale
Pour calculer la variance attendue, notée Var(X), nous utilisons la seconde relation sur la variance présentée au cours 2.4 :
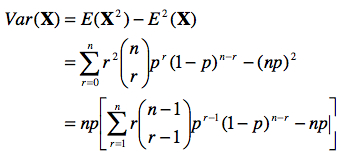
À nouveau, posons k = r – 1.
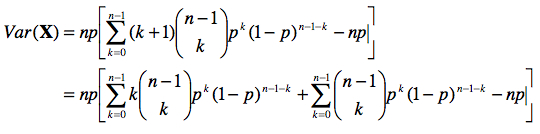
Le premier terme entre crochets représente la moyenne d’une variable qui serait binomiale entre 0 et n – 1. Posons Y ~ B(n – 1, p). Le second terme se résout suivant la relation (a) notée à la sous-section précédente.
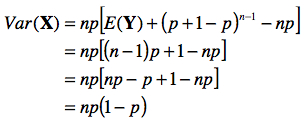
c. Autres moments statistiques
Suivant une méthode similaire, on peut aussi résoudre l’asymétrie attendue Sk(X) et la kurtose attendue Ku(X). On obtient :
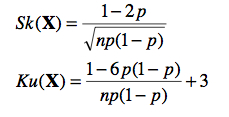
De fait, on vérifie qu’avec 35 machines (n = 35) et la possibilité d’une machine en panne à 1 / 100 (p = 0.01), on s’attend à ce que le nombre moyen de machines en panne dans l’usine soit de 0.35 avec une variance de 0.3465 (soit un écart type de près de 0.59) et une asymétrie de 1.66, soit une distribution très décalée vers la gauche.
Section 3. La distribution normale
Dans cette section, nous considérons une distribution dans laquelle les résultats possibles sont tous les nombres réels (pas seulement les nombres entiers positifs, comme dans le cas de la Binomiale). Cette distribution est appelée la distribution normale ou encore gaussienne (du nom de son inventeur, Carl Friedrich Gauss). Tout comme la binomiale, il s’agit d’une distribution parmi une infinité d’autres possibles. La normale n’est pas une loi de la nature que l’on observe réellement. Il s’agit en fait d’une théorie basée sur des postulats simples, que nous allons survoler plus tard (en science, plusieurs concepts ne sont pas parfaitement vrais mais donnent des approximations très utiles).
4.1. Fonction de masse et paramètres
La distribution normale est spécifiée par la formule mathématique de sa PDF :
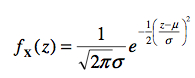
(Dans cette formule, on divise par √2π car sinon l’aire totale sous la courbe serait de √2π alors qu’en probabilité, l’aire totale doit être de 1). Cette fonction est souvent représentée par la familière courbe en forme de cloche que l’on retrouve à la Figure 4.
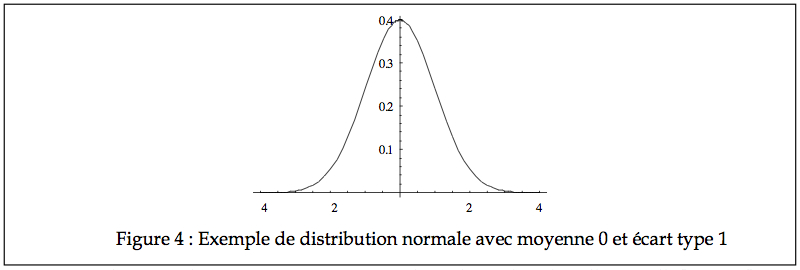
La courbe normale est continue pour toutes les valeurs de z dans l’intervalle ]-∞ , +∞[, de telle façon que tous les intervalles possibles ont une probabilité plus haute que zéro. Pour cette raison, il est préférable de représenter graphiquement la normale avec une courbe continue plutôt qu’avec des histogrammes. Cette distribution est parfaitement et toujours symétrique, de telle façon que la moyenne, la médiane, et le mode coïncident. L’aire totale sous la courbe égale toujours 1 puisqu’il s’agit de la probabilité qu’un événement (n’importe lequel) se produise.
La distribution normale est une famille de courbes puisqu’une courbe normale peut se distinguer d’une autre par la position (Figure 5, gauche), par l’échelle (Figure 5, centre) ou par les deux à la fois (Figure 5, droite). Ce qui distingue une courbe normale d’une autre sont les paramètres de la population, qui sont au nombre de deux : la position μ et l’échelle σ. Pour faire plus court, on note que X ~ N(μ, σ).
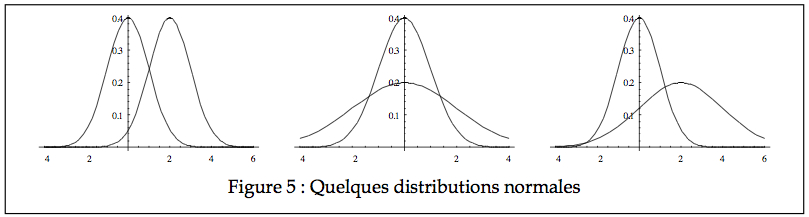
La fonction atteint son maximum (le mode) quand l’exposant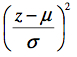 
est minimum.
C’est donc dire que la moyenne est aussi atteinte quand z vaut μ, donc 
= μ. On peut aussi prouver ce résultat comme nous l’avons fait pour la binomiale en utilisant la définition de ,
soit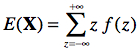 
.
Cependant, z est continue et ne prend pas uniquement les valeurs entières ] … -3, -2, -1, 0, 1, 2, 3, …[. Il faut donc procéder avec des intervalles infiniment petits, ce que permet le calcul infinitésimal (lui aussi inventé par Gauss). On doit donc résoudre.
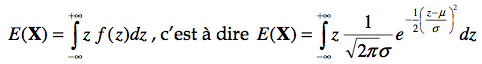
Heureusement, cette formule se résout assez facilement, et on obtient que E(X) = μ tel qu’attendu. De la même façon, on résout
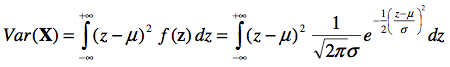
pour obtenir que Var(X)=σ2. Donc, le paramètre d’échelle σ décrit parfaitement la variance de la population.
4.2. Probabilité d’un événement normalement distribué
Avec la distribution binomiale, l’on pouvait dire que fX (r) indique la probabilité d’obtenir r succès. Cependant, pour la distribution normale (et toute fonction continue), fX (z) n’est pas interprétable. En effet, fX ( z ) = Pr { X = z }. Cependant, pour un nombre réel, quelle est la probabilité d’obtenir exactement une valeur précise z? Même si je vous donnais un temps infini, la probabilité que vous puissiez me dire exactement le nombre π est nulle. De même, dans une population où la taille moyenne des individus est de 1m75, quelle est la probabilité que vous échantillonniez un individu mesurant exactement 1m75 (c’est à dire 1.75000000000000000000000000000… mètre)? De fait, Pr { X = z } (la probabilité d’échantillonner un individu mesurant exactement z m) est zéro peu importe z.
Par contre, on peut se demander quelle est la probabilité que notre variable aléatoire soit approximativement z, c’est à dire, Pr { X ≈ z } = Pr { z – ∆z X ≤ z + ∆z} où ∆z indique la précision voulue. Sur un graphique, on verrait ceci comme l’aire d’une section de la courbe normale. Le calcul d’une aire sous une courbe peut être difficile, mais la tâche nous est grandement facilitée par les fréquences cumulatives. Voir la Figure 6.
Par définition, une fréquence cumulative donne la probabilité qu’une variable aléatoire soit inférieure à une valeur z, ce que l’on note par FX ( z ). En faisant la différence FX (z + ∆z) − FX (z − ∆z) , on obtient la probabilité que X soit inférieur à z + ∆z, mais pas
inférieur à z – ∆z, ce qui est bien ce que l’on recherche. Il est clair de cet exemple que pour des variables continues, la fonction de distribution cumulative (CDF) est la plus utile.
4.3. Pourquoi la normale?
Il existe trois raisons d’utiliser la normale. Premièrement, la normale est une très bonne approximation de la distribution Binomiale quand n est grand. Deuxièmement, la normale est la distribution prédite quand il existe plusieurs sources d’erreurs dans nos données. Finalement, à cause du théorème central limite. Dans ce qui suit, nous élaborons à propos des deux premières raisons, et gardons le théorème central limite pour le cours 5.
a. Approximation de la distribution binomiale
Calculer la distribution binomiale peut être assez fastidieux quand le nombre d’essais de Bernoulli est grand (n >>). Pour cette raison, une approximation est souhaitable. L’approximation que nous présentons ici n’est valide que lorsque p ≈ 1⁄2 (toute approximation faite quand n >> est appelée une approximation asymptotique. Nous verrons d’autres exemples d’approximations asymptotiques).
Soit X ~ B(n, p). Puisque E(X) = n p et Var(X) = n p(1–p), nous allons poser Y ~ N( n p,√n p(1-p) ). On peut montrer formellement que lorsque n >> , l’écart entre la probabilité prédite par fX(z) et FY (z +1/ 2) − FY (z −1/ 2) se réduit à zéro. La preuve est cependant trop longue pour la mettre ici. Nous allons plutôt montrer un exemple où n est modérément grand et voir que la différence est déjà très faible.
Dans le tableau qui suit, nous illustrons les probabilités pour les 16 cas possibles de succès quand n = 15. Dans cet exemple, p = 1⁄2 exactement. Comme on le voit, l’écart entre la binomiale X et la normale Y est insignifiant (de l’ordre du millième). Il est cependant légèrement plus grand aux extrémités puisque la normale s’étend de –∞ à +∞, contrairement à la binomiale.
Une autre façon de montrer que la normale est identique à la binomiale pour n >> quand p est 1⁄2 est de regarder les moments statistiques. En effet, si les deux distributions ont les mêmes valeurs pour tous les moments (moyenne, variance, skewness, kurtose, et tous les autres), alors forcément il s’agit de la même distribution (il s’agit d’un théorème prouvé dans Cramér).
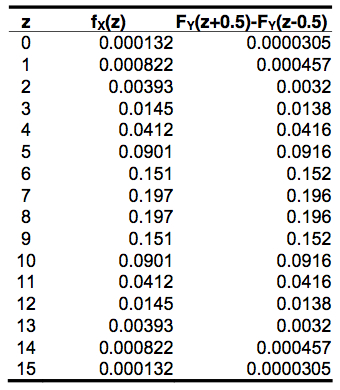
Avec la définition de X et de Y ci-haut, on peut faire le tableau qui suit des quatre premiers moments :
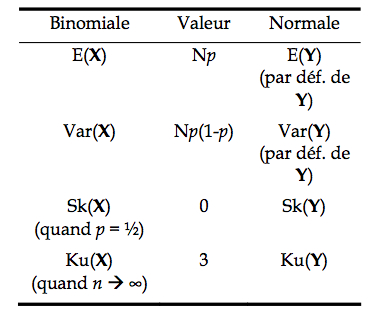
Comme on le voit, les quatre premiers moments correspondent parfaitement, et si l’on continuait avec les autres moments, la correspondance continuerait indéfiniment. Dans ce qui précède, on entend par n >> un n supérieur à 20.
b. Plusieurs sources d’erreurs
Supposons que la mesure de chacune de nos données brutes soit entachée d’un grand nombre d’ « erreurs » qui affectent le score véridique que l’on aurait obtenu. Ces nombreuses sources d’erreurs peuvent être liées à des mesures imprécises ou (en psychologie) peuvent être liées à des facteurs tels l’attention, les préoccupations du sujet, l’historique du sujet, etc. qui viennent tous modifier légèrement sa vraie performance.
Notons alors X le score mesuré et T le score réel du sujet. Nous avons que X = T + e. Notons qu’ici, T n’est pas une variable aléatoire puisqu’il s’agit du score idéal du sujet. La variable aléatoire e est la source d’aléa qui rend X une variable aléatoire. Pour illustrer le fait que e reflète un grand nombre de sources d’erreurs, posons
e=g×(e1 +e2 +e3 +…+eN)
où chaque source d’erreur ei est soit présente et réduit la performance du sujet ou absente et favorise une bonne performance. Le but de la constante g est de mettre sur l’échelle des performances (en point de QI, en terme de vitesse, etc.) l’effet cumulé des erreurs tel que dans l’absence d’erreur, la performance ne soit pas affectée. Nous avons donc que ei = +1 ou ei = -1.De plus, nous postulons que Pr{ei = +1}≈1⁄2.
Rendu à ce point, vous devriez voir où je m’en vais : chaque source d’erreur est un essai de Bernoulli!
Regardons quel est le nombre d’erreurs moyen, où Z indique le nombre de source d’erreurs positives, et n – Z le nombre de sources d’erreurs négatives :
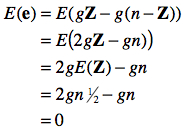
Les erreurs favorables et défavorables s’annulent mutuellement en moyenne. De plus, la variance se calcule aussi par
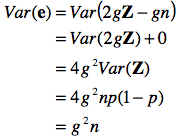
Ceci posé, nous trouvons donc que E(X) = E(T + e) = T+E(e) = T et que Var(X) = Var(T + e) = Var(e) = g2. De fait, la variabilité observée dans X résulte uniquement de la variabilité dans e qui est binomiale. Comme on postule que n >>, la variabilité de e est approximée par une distribution normale, d’où il s’ensuit selon nos postulats que X est normalement distribué (X ~N( T, g2n) ).
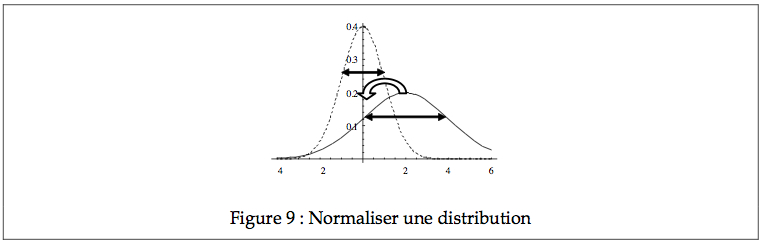
Transformation linéaire
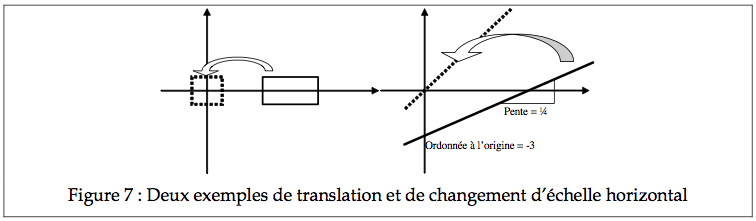
Il est parfois utile, pour simplifier le traitement d’un objet mathématique, de changer sa position de façon à ce qu’il se présente sous un format plus standard (format canonique). Par exemple, dans l’exemple ci-contre, il est plus simple de déplacer le rectangle de façon que son centre coïncide avec l’origine de l’abscisse. Déplacer un objet (exécuter une translation) s’effectue simplement en soustrayant la différence entre la position actuelle et la position voulue de l’objet (par exemple ici, on peut vouloir déplacer de 3 cm). Similairement, on peut changer l’étendue d’une forme en divisant la mesure de son étendue.
En terme mathématique, on transforme une variable x en une variable x’ avec cette simple transformation où p est la position originale et e est l’étendue :
Par exemple, ci-contre, l’on transforme la droite dont l’équation est y = 1/ 4x − 3 en posant
on vérifie facilement que la droite transformée résultante est
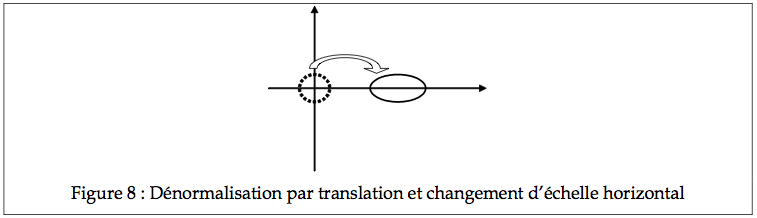
Une transformation peut aussi procéder à l’envers pour transformer une courbe canonique en une forme plus élaborée, par exemple, pour passer du cercle à l’ellipse. Supposons que l’on souhaite déplacer le cercle de 3 cm vers la droite (p) et étirer le grand axe du double (e). L’équation du cercle étant : y2 =1− x2 , on observe que
y‘2 = 1-x‘2=
qui est bien l’équation d’une ellipse.
De la même façon, on peut déplacer des distributions. Soit une distribution dont la position (la tendance centrale) se trouve à 2 cm, et l’étendue (l’écart type) est de deux unités.
En changeant x pour x’ comme précédemment, on se trouve à ramener la distribution au centre, et son échelle à 1. Dans le cas d’une normale N(2, 2), on se trouve à réduire tous les scores de deux (i.e. un déplacement p égal à la moyenne μ), donc, la moyenne devient 0, et on réduit aussi l’étendue par 2, d’où l’écart type devient 1. On vérifie facilement en calculant l’espérance et la variance avec les formules usuelles :
Ainsi, si X ~ N(2, 2), alors X’=(X-μ)/σ ~ N(0, 1). Lorsqu’on applique une transformation linéaire à une variable aléatoire dans le but de transformer sa distribution en une distribution canonique, on va parler de standardisation. (Notez qu’ici, la distribution la plus simple est N(0, 1) et non pas N(0, 0). Voyez-vous pourquoi?).
La standardisation peut être effectuée peu importe la forme de la distribution. Cependant, seulement la position et l’échelle sont affectées par une telle transformation. Si la distribution est asymétrique avant la normalisation, elle le restera après.
4.4. Distribution normale standardisée
Pour faciliter l’étude des caractéristiques de la loi normale et surtout pour pouvoir déterminer rapidement les proportions sans devoir construire une infinité de courbes correspondant à toutes les moyennes et écarts types possibles, nous utilisons toujours la distribution normale standardisée, encore appelée la distribution normale centrée réduite.
L’observation du graphique de la Figure 10 permet d’apprécier la relation entre l’écart type et le pourcentage de l’aire sous la courbe : une proportion de 34% de l’aire totale (donc 34% de toutes les possibilités) se situe entre 0 écart type (la moyenne) et 1 écart type; 68% entre –1 et +1 écart type; seulement 2% des cas se situent au dessus de 2 écarts types, et à peu près trois cas sur 1000 (0.26%) sont soit au dessus, soit en deçà de trois écarts types.
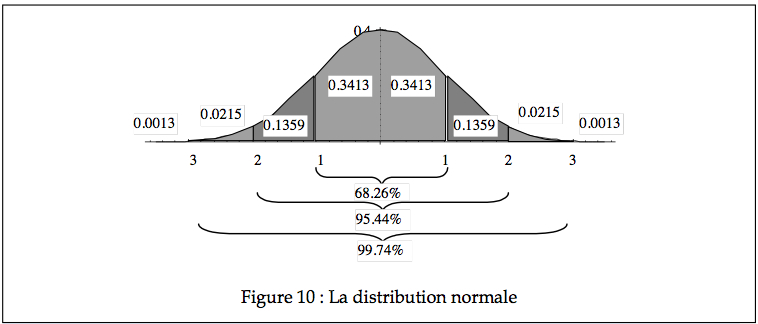
La transformation linéaire vue plus haut, dans le cas d’une variable aléatoire de type normale, est souvent appelée une cote z, ou encore un score z. N’importe quel Xi normalement distribué peut être exprimé en cote z (on devrait plutôt noter Zi, puisque Z est
aussi une variable aléatoire). En se référant à la courbe normale standardisée, on peut obtenir un estimé de la fréquence de cette valeur, c’est à dire sa probabilité dans la population. Par exemple, si un groupe d’étudiants obtient à un examen une moyenne de 70 et un écart type de 10 (et si les résultats sont bien distribués normalement), on peut conclure que 68% des notes devraient se trouver entre 60 et 80 (± 1 écart type), qu’une note de 90% ou plus (supérieure à 2 écarts types) devrait être obtenue par environ 2% des étudiants, et qu’une note de 40 (en bas de 3 écarts types) est vraiment exceptionnellement mauvaise.
Une autre information importante peut être obtenue par la transformation de données brutes en cotes z. Comme chaque variable est alors mesurée sur la même échelle et présente la même moyenne, elles deviennent comparables. Par exemple, une note de 75 en mathématique et une note de 72 en français peuvent sembler similaires. Cependant, si l’on sait que la moyenne du groupe en math est de 60 avec un écart type de 5, et que la moyenne en français est de 75 avec un écart type de 5, on découvre un génie des maths et un piètre écrivain.
Section 5. La distribution de Weibull
La binomiale vue au début de cette section s’intéresse à des événements du type « obtenir r succès parmi n essais de Bernoulli », i.e où r est le nombre de succès parmi n événements.
Postulons plutôt que : a) chaque événement donne une valeur réelle positive plutôt qu’une valeur binaire, et b) que je suis intéressé par le plus petit (ou le plus grand) de ces n événements. Un exemple s’observe lors d’une course de 100m « obtenir un meilleur temps de 9 s quand 10 coureurs compétitionnent ». Les coureurs perdant ont bien un temps, mais n’étant pas le meilleur temps, il est rejeté.
L’exemple typique nous provient de la Hollande. Ce pays est en grande partie sous le niveau de la mer, et des barrages de 6 mètres protègent les habitants. Que survienne une marée supérieure à la hauteur des barrages (comme en 1952), et c’est la catastrophe. On veut donc connaître la probabilité de l’événement « la plus haute marée est de 6 mètres parmi les 365 marées de l’année ».
Un autre exemple pertinent pour la neuropsychologie nous vient de l’étude du déplacement de l’influx nerveux. Selon une vision, les influx nerveux sont très redondants, voyageant sur un grand nombre de fibres parallèles d’une aire du cerveau à l’autre. Cependant, certains postulent que seuls les signaux les plus rapides sont cruciaux. La question est donc de connaître la distribution des événements « le temps du plus rapide signal parmi les milliers de signaux redondants ».
5.1. Fonction de masse et paramètres
On démontre (mais je saute les détails) qu’avec seulement les deux postulats a) et b) ci- haut, on peut déterminer la forme de la distribution. Il s’agit d’une loi lentement asymptotique (i. e. pour n >>>, c’est à dire plus de 100 sous-événements) que l’on nomme la distribution de Weibull (du nom de l’ingénieur qui l’a introduit dans l’étude des matériaux). Sa fonction de masse est donnée par l’équation :
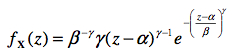
pour laquelle on note X ~ W(α, β, γ). La distribution de Weibull nécessite trois paramètres pour être dessinée, soit α, β, et γ. Le premier représente la position de la distribution, soit l’endroit où elle débute, le second représente l’échelle de la distribution (est similaire mais pas numériquement équivalent à l’écart type), et le dernier est la forme de la distribution, soit son degré d’asymétrie (encore une fois, similaire mais pas numériquement équivalent à la skewness).
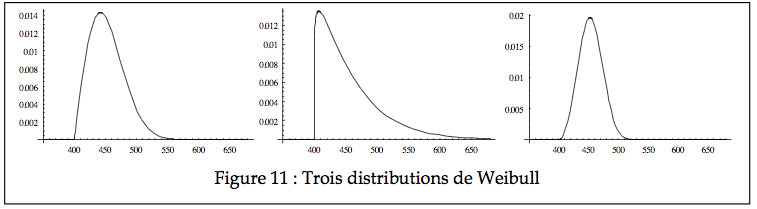
Les images de la Figure 11 illustrent trois Weibull avec comme forme 2, 1.1, et 3 respectivement. Toutes ont la même échelle (60) et la même position (400). Après normalisation, elles partiraient toutes à zéro et auraient une échelle de 1, mais seraient néanmoins de formes différentes.
5.2. Moments statistiques
On peut démontrer que
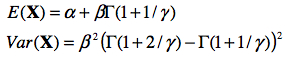
Section 6. La distribution χ2
Supposons que nous ayons un échantillon X = {X1, X2, X3, … XN} tiré d’une population normalement distribuée (X ~ (μ, σ) ). Une façon de synthétiser cet échantillon est de calculer la moyenne. Cependant, nous avons vu précédemment que l’on peut normaliser les données avec la formule
Qu’advient-il si l’on décide de calculer une statistique totalement arbitraire, que l’on appellera G, calculé par la formule :
G =
X‘i
Comme nous l’avons vu au cours 2, il s’agit d’une somme (normalisée) des écarts à la moyenne, qui donne toujours zéro. Cette statistique n’est donc pas intéressante. Regardons plutôt une autre statistique, que l’on appelle G2 (ici, le carré fait partie du nom, et ne signifie pas qu’il faut mettre la valeur de G précédente au carré), calculée par
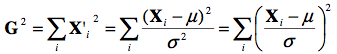
c’est à dire la somme des carrés des scores normalisés. Bien que cette statistique semble arbitraire, a) il s’agit bien d’une statistique puisqu’elle retourne une valeur synthétisant un échantillon, b) on verra plus loin (cours 6) qu’elle peut être très utile dans certains cas.
6.1. Fonction de masse et paramètre
On démontre (mais encore une fois, on saute les détails) que la statistique G2 possède une distribution théorique que l’on appelle la χ2. Soit une variable G2 ~ χ2(n), la fonction de masse est donnée par la formule :
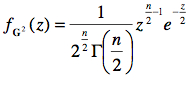
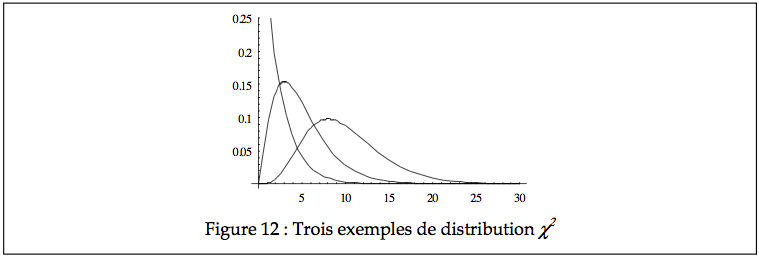
La distribution χ2 est entièrement définie par le paramètre n, le nombre d’items additionnés. n est donc le seul paramètre pour décrire la population des tous les G2 possibles. Ce n détermine la forme de la distribution, comme on le voit ci-bas pour n = 2, 5, et 10.
6.2. Moments statistiques
Puisque pour chaque score Xi, on soustrait μ avant de mettre au carré, on se retrouve en fait à calculer E(Xi – ) (voir fin du cours 2), qui donne la variance. Donc, le résultat attendu pour un Xi’2, soit E(Xi’2), est de 1, puisque la variance est de 1.Il découle que pour la somme de n tel score, E(G2) = n. On démontre aussi que la variance Var( G2) = 2 n. On voit intuitivement ces mesures sur le graphique ci-haut, où autant le point d’équilibre que l’échelle des distributions χ2 croît avec le paramètre n.
De plus, la skewness et la kurtose sont données par
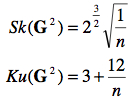
Comme on le voit, plus n s’accroît, plus les moments deux et trois tendent vers 0 et 3 respectivement. C’est à dire que pour n >> la distribution χ2(n) tend à devenir identique à la distribution normale N (n, 2 n).
Section 7. La distribution de Fisher F
La distribution N suppose que nous avons deux échantillons tirés d’une même population, X = {X1, X2, X3, … Xnx} et Y = {Y1, Y2, Y3, … Yny}, où X ~ N(μ, σ} et Y ~ N(μ, σ}. Si l’on calcule du premier échantillon la statistique G2X comme précédemment et que l’on divise par NX, on devrait obtenir une statistique dont la moyenne est autour de 1. On fait de même pour Y, et on prend le ratio du premier sur le second pour obtenir une statistique F. La formule complète est donc :
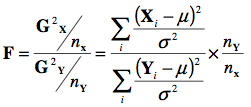
pour laquelle on dit que F ~ F (nX, nY). Cette distribution est asymétrique pour nX ou nY petit. On remarque que le paramètre σ s’annule puisque par hypothèse, il s’agit du même σ au numérateur et au dénominateur :
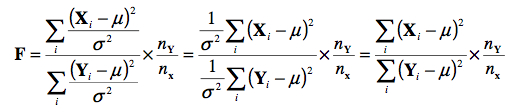
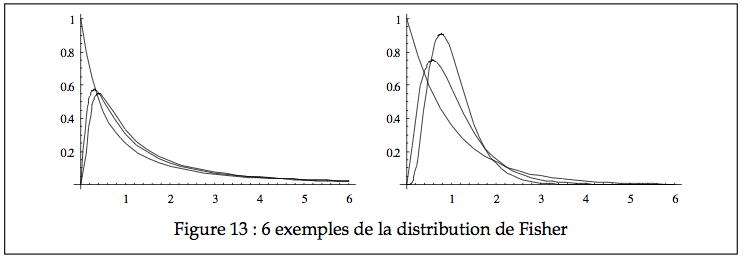
À la Figure 13, on voit une illustration pour nX = 2, 5, et 10 pour nY = 2 (gauche) et 50 (droite).
7.1. Fonction de masse et paramètre
La fonction de masse de la distribution de Fisher est donnée par :
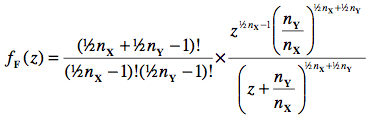
7.2. Moments statistiques
La moyenne de cette distribution n’est pas exactement 1, mais tend vers cette valeur quand l’échantillon utilisé au dénominateur est grand. De plus, quand nX et nY sont grands, la variance tend vers zéro, la skewness vers 0 et la kurtose vers 3. Donc, cette distribution tend à devenir normale pour de grands échantillons. Formellement,
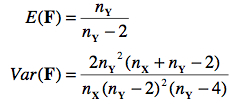
Comment lire une table statistique
Certaines distributions de fréquence sont facilement calculables avec une calculatrice (par exemple, la binomiale). D’autres par contre, ne le sont virtuellement pas (par exemple, la χ2 avec sa fonction Γ -combien savent que Γ( 1⁄2 ) = √π ?-. On peut alternativement utiliser un logiciel, tel Mathematica ou Excel, pour calculer ces valeurs à chaque fois que c’est nécessaire. Cependant, ces logiciels sont d’introduction récente et n’étaient pas accessibles (ou n’existaient tout simplement pas) il y a seulement 10 ans. Pour cette raison, on retrouve fréquemment des tables où les calculs ont déjà été réalisés.
La première chose à comprendre quand on regarde une table est de bien saisir quelle sorte de valeur est tabulée.
En général, pour une variable aléatoire discrète (qui ne prend que des valeurs entières, telle la binomiale), on présente la probabilité d’un événement précis, que l’on note : fX ( r ) = Pr{ X = r }. Il faut lire : la probabilité que la variable aléatoire X prenne la valeur r. C’est ce que l’on retrouve dans la Table 1 (sur le site web).
Dans le cas d’une variable aléatoire continue (qui peut prendre toutes les valeurs réelles, tel la normale, la χ2 et la ), on présente plutôt les probabilités cumulatives, que l’on note : FX ( z ) = Pr{ X ≤ z }, c’est à dire la probabilité que la variable aléatoire X prenne une valeur inférieure ou égale à z. La Table 2 présente un tel exemple avec la distribution normale standardisée. Puisqu’il n’y a pas de paramètre pour cette courbe, une simple table de FX ( z ) en fonction de z suffit.
Dès que la distribution que l’on veut tabuler possède des paramètres (telle la χ2), la table devient de taille gargantuesque puisqu’il faut varier autant z que le paramètre (ν pour la χ2 ). Cependant, puisque la χ2, la , et même la t (que l’on verra au cours 5) ne sont utilisées que pour des fins de tests statistiques, on va plutôt procéder à l’envers : Tabuler la valeur de z pour laquelle FX ( z ) égale une valeur cible. En statistique inductive (cours 4), on est souvent intéressé par des valeurs limites, par exemple la valeur z tel que 95% des observations devraient être inférieures. Pour confondre les étudiants, on va inverser et chercher le z tel que 5% des observations soient supérieures (c’est bien la même chose). On a donc z en fonction du paramètre et en fonction de la probabilité cible 1-FX (z)=Pr{X≥z}.Les tables 3, 4, et 5 sont construites de cette façon.
Exemple d’utilisation de la table normale standardisée
Dans une installation de 5000 ampoules électriques, on a constaté que la vie moyenne des ampoules était de 1200 heures avec un écart type de 200 heures. Ici, si on établissait un échantillon, chaque donnée brute Xi serait en fait l’heure à laquelle l’ampoule a grillé, et notre échantillon Xi serait un ensemble contenant des nombres d’heures pour qu’une ampoule grille. Formellement, on a C3m = 1200 heures et n C3m2 = 200 heures. Implicitement, on postule que la population est normalement distribuée.
1) Combien peut-on prévoir d’ampoules hors d’usages au bout de 900 heures?
Ces 900 heures, en termes d’écart type correspondent à (900-1200)/200 = -1.5. Le signe moins signifie qu’il s’agit d’une cote z inférieure à la moyenne (bien entendu, puisque 900 < 1200). Les négatifs ne sont pas présents sur la table, mais puisque la courbe est parfaitement symétrique, on trouve F(-1.5) = 1 – F(1.5) = 1-0.933 = 0.067. Il s’agit de la proportion attendue des ampoules qui vont griller avec 900 heures. Puisque nous en avons 5000, 6.7% × 5000 donne 335 ampoules.
2) Combien d’ampoules seront hors d’usage en environ 1300 heures ± 200 heures?
On veut connaître le nombre de pannes ayant lieu avant 1500 heures, mais ayant eu lieu après 1100 heures. Ces nombres, une fois normalisés, nous donnent zmax = 1.5 et zmin = -0.5. Pour zmax la proportion de pannes ayant lieu avant est de 0.933, auquel il faut soustraire la proportion des ampoules qui seraient tombées en panne avant zmin, dans une proportion de 0.309. La différence est de 0.624, soit 62.4%. Sur une population de 5000, ça donne 3120 ampoules.
3) Combien de temps faut-il attendre pour avoir 20% d’ampoules en panne?
Ici, on cherche le z tel que 20% des valeurs seront inférieures. Ce sera certainement une valeur négative (en bas de la moyenne) puisque à la moyenne, 50% des cas sont déjà couverts. Comme la table est symétrique, on cherche la valeur positive qui excède 80% (1 – 20%), et on mettra un signe moins devant ce nombre. En regardant dans la table, la valeur z tel que nous sommes le plus près de 80% est 0.84. –0.84 est donc un nombre d’heures (en score standardisé) tel que 20% des ampoules flanchent auparavant. Si l’on « dé normalise », on obtient : -0.84 × n C3m2 + C3m , soit 1032 heures.
Exercices
1. Concernant la distribution normale, laquelle de ces affirmations est fausse :
a) Elle est la base de plusieurs analyses statistiques
b) Les mesures se situent généralement à l’intérieur de 3 ou 4 écarts types
c) L’aire sous la courbe correspond à la probabilité
d) La probabilité d’apparition d’un événement décroît avec la distance à la moyenne
e) Aucune n’est fausse
2. La cote z est l’écart d’une mesure à la moyenne divisé par l’écart type
a) Vrai
b) Faux
3. Une cote z grande a une faible probabilité de se produire
a) Vrai
b) Faux
4. Dans un test de dix questions, on veut prélever un échantillon de 3 questions pour fin de vérification. Combien d’échantillons est-il possible de prélever?
5. Une distribution normale est nécessairement symétrique autour de sa moyenne
a) Vrai
b) Faux
6. Lors d’un tirage au sort, il y a plus de chance que la valeur obtenue soit située près de la moyenne, peu importe la population
a) Vrai
b) Faux
7. Une fréquence relative élevée implique une faible probabilité
a) Vrai
b) Faux
8. Quelle caractéristique s’applique à une distribution dont les mesures brutes qui se distribuaient normalement ont été transformées en cote z?
a) Sa moyenne est égale à 0
b) Sa variance est de 1
c) Elle est en forme de cloche
d) aetbs’Appliquent
e) a, b, et c s’appliquent.
9. Lorsque vous lancez 10 pièces de monnaie, quelle est la probabilité d’obtenir 0, 1, 2, ou 3 faces?
a) 0.001
b) 0.011
c) 0.010
d) 0.117
e) 0.172
10. En lançant 15 pièces de monnaies, quelle est la probabilité d’obtenir exactement 10 faces?
a) 0.0916
b) 0.015
c) 0.153
d) 0.916
e) aucune de ces réponses
11. En lançant un dé, quelle est la probabilité d’obtenir un six?
12. Une probabilité peut être exprimée sous forme de pourcentage
a) Vrai
b) Faux
13. La fréquence relative associée à un événement correspond à la probabilité de cet événement
c) Vrai
d) Faux
Soit une distribution dont la moyenne est de 40 et l’écart type de 10;
14. Normalisez ces valeurs :
a) 44
b) 36
c) 45.2
d) 0
e) 10.40
15. Trouvez les valeurs réelles correspondant aux valeurs normalisées suivantes :
a) –2.00
b) –1.90
c) 2.00
d) 3.00
e) 10.40
Cent étudiants ont subi un examen où la moyenne du groupe est de 75% avec un écart type de 8. Les résultats se distribuent normalement.
16. Quelle proportion des étudiants a environ 80% (entre 75% et 85%)?
17. Quelle est la probabilité qu’un étudiant ait une note supérieure ou égale à 90% ?
18.Quelle est la probabilité qu’un étudiant soit plus de deux écarts types en bas de la moyenne?
19. Combien s’attend-t-on à avoir d’étudiants avec une note entre 85% et 90%?
20. À table, avec 5 convives, quelqu’un propose un toast. Combien entend-t-on de verres se frapper?
21. Combien existe-t-il de combinaisons qui permettent de former une équipe de 5 joueurs avec une banque de 10 noms?
22. Dans une distribution normale standardisée, quelle proportion des cas sera comprise entre la moyenne et le score suivant :
a) –2.0:
b) +0.5:
c) +1.0:
d) +2.0:
e) +3.0:
23. Dans une distribution normale standardisée,quelle proportion des cas sera située au-dessus des scores suivant :
a) –2.0:
b) +0.5:
c) +1.0:
d) +2.0:
e) +3.0:
24. Postulant une distribution normale dont la moyenne est 80, l’écart type est de 8, et n = 150, pour quel score s’attend-t-on à trouver des individus avec un score inférieur
a) 126 personnes
b) 12
c) 63
d) 75
e) 150
25. À supposer qu’il existe un test psychologique valide se distribuant normalement et ayant une moyenne de 100 et un écart type de 10, en dessous de quel score se trouve des participants :
a) 10%
b) 5%
c) 1%
26. Étant donné un groupe de 500 participants de 11 ans ayant obtenus à un test une moyenne de 48 avec un écart type de 8 et un groupe de 800 participants de 14 ans ayant obtenus au même test une moyenne de 56 et un écart type de 10, et postulant la normalité des scores
a) Combien de participants de 11 ans ont un résultat supérieur à la moyenne obtenue chez les 14 ans?
b) Combien de 14 ans ont des résultats inférieurs à la moyenne obtenue chez les 11 ans?
27. La moyenne de toutes les cotes z individuelles est la même chose que la moyenne des données brutes ensuite transformée en cote z?
a) Vrai
b) Faux
Si vous remarquez des informations erronées ou manquantes, merci de le partager par les Commentaires.